 Uma brilhante e
voraz rã quer atravessar o rio, pois do outro lado viu um delicioso
insecto do qual pretende fazer o seu almoço. Para conseguir lá chegar,
em vez de nadar, optou por ir saltando de nenúfar em nenúfar até à
outra margem.
Uma brilhante e
voraz rã quer atravessar o rio, pois do outro lado viu um delicioso
insecto do qual pretende fazer o seu almoço. Para conseguir lá chegar,
em vez de nadar, optou por ir saltando de nenúfar em nenúfar até à
outra margem.
 Uma brilhante e
voraz rã quer atravessar o rio, pois do outro lado viu um delicioso
insecto do qual pretende fazer o seu almoço. Para conseguir lá chegar,
em vez de nadar, optou por ir saltando de nenúfar em nenúfar até à
outra margem.
Uma brilhante e
voraz rã quer atravessar o rio, pois do outro lado viu um delicioso
insecto do qual pretende fazer o seu almoço. Para conseguir lá chegar,
em vez de nadar, optou por ir saltando de nenúfar em nenúfar até à
outra margem.
A rã só consegue saltar no máximo S dm. Por outras palavras, só consegue saltar de um nenúfar para outro se a distância entre eles for menor ou igual a S dm. Recorda que a distância entre dois pontos (Y1, X1) e (Y2, X2) é dada pela raíz quadrada de [(Y1- Y2)2 + (X1-X2)2]. Do mesmo modo, a rã só consegue saltar da margem inicial para um nenúfar (ou de um nenúfar para a margem final) se a distância entre a margem e o nenúfar for menor ou igual a S dm.
De cada vez que dá um salto muito grande a rã perde alguma energia. De facto, por cada salto maior que metade da sua capacidade máxima de salto S, a rã gasta uma caloria. A rã inicia a sua travessia exactamente com E calorias de energia armazenadas no seu corpo, pelo que se necessitar de fazer E saltos mais longos do que a metade da sua capacidade de salto, o seu nível de energia atinge o zero e rã fica demasiado exausta para prosseguir a sua jornada e lá se vai o almoço. Por isso mesmo ela tem de planear a viagem de maneira a que nunca fique com energia igual a zero, nem que seja no preciso momento em que atinge a outra margem.
A rã começa sempre na margem esquerda do rio e quer atravessar para a margem direita. Para te ajudar, o mapa do rio pode ser pensado como um plano de largura L dm e altura A dm. O rio tem uma largura de exactamente L dm. A margem esquerda do rio termina na linha formada por X=0 e a margem direita, aonde a rã quer chegar, começa com a linha formada por X=L. Os nenúfares são dados por pares de coordenadas (Xi, Yi). A figura seguinte ilustra um mapa exemplo de 8 dm de largura por 7 dm de altura, com 10 nenúfares:
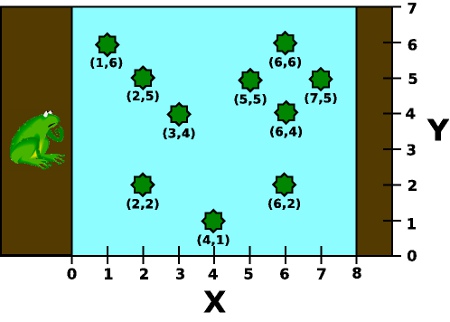
O objectivo da rã é chegar da margem esquerda à direita dando o mínimo número de saltos que for possível. Por exemplo, para o mapa da figura, se a rã tiver uma capacidade de salto de 3 dm e começar com 2 calorias de energia, o mínimo de saltos que tem de fazer é 6. Um caminho de 6 saltos (existem vários) seria por exemplo:
Local: Margem Esq. | -> |(1,6)| -> |(2,5)| -> |(5,5) | -> |(6,6)| -> |(7,5)| -> | Margem Dir. Energia: 2 | -> | 2 | -> | 2 | -> | 1 | -> | 1 | -> | 1 | -> | 1 Distância salto: | 1 | |~1.4| | 3 | |~1.4| |~1.4| | 1 |
Se a rã tivesse a mesma capacidade de salto, mas tivesse inicialmente 3 calorias de energia, então conseguiria fazer um caminho com apenas 4 saltos. Por exemplo, poderia fazer o seguinte:
Local: Margem Esq. | -> |(2,2)| -> |(4,1)| -> |(6,2) | -> | Margem Dir. Energia: 3 | -> | 3 | -> | 2 | -> | 1 | -> | 1 Distância salto: | 2 | |~2.2| |~2.2| | 2 |
Se existirem vários caminhos que gastem o mínimo número possível de saltos, a rã escolhe aquele onde chega ao final com a maior quantidade possível de energia. Se mesmo assim existirem vários caminho empatados, qualquer um serve.
Dada a capacidade S de salto da rã, a sua energia inicial E, um mapa de um rio com largura L e altura A e a localização de N nenúfares indicados cada um pelas suas coordenadas (Xi, Yi), a tua tarefa é descobrir o caminho que leva a rã da margem esquerda para a margem direita com o mínimo número de saltos que for possível. Em caso de empate, deves escolher o caminho que leva a rã a terminar com a maior quantidade de energia que for possível.
Na primeira linha do input vêm dois números inteiros S e E, indicando a capacidade de salto da rã (em dm) e a sua energia inicial (em calorias), respectivamente.
Segue-se uma linha com exactamente dois número inteiros L e A indicando a largura e altura (em dm) do mapa do rio a considerar, respectivamente.
Segue-se uma outra linha contendo um único número inteiro N indicando o número de nenúfares no rio.
Depois vêm exactamente N linhas, cada uma com dois números inteiros Xi e Yi, separados por um único espaço, indicando a localização do i-ésimo nenúfar. Os nenúfares podem vir por qualquer ordem e são todos distintos.
O output deve ser constituído por uma única linha contendo dois números inteiros separados por um espaço indicando o número mínimo de saltos para a rã chegar da margem esquerda à margem direita e a máxima energia com a rã consegue chegar à margem direita gastando esse número mínimo de saltos, respectivamente.
Em todos os casos de teste é possível chegar à margem direita com energia positiva. Note que pode dar-se o caso de apenas com um salto válido a rã atingir a margem direita directamente, sem passar por nenhum nenúfar.
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| 1 ≤ S ≤ 1 000 | Capacidade de salto da rã | |
| 1 ≤ E ≤ 20 | Energia inicial da rã | |
| 1 ≤ A,L ≤ 1 000 | Altura e largura do mapa | |
| 1 ≤ N ≤ 20 000 | Quantidade de nenúfares | |
| 0 < Xi < L | Posição em largura de um nenúfar | |
| 0 < Yi < A | Posição em altura de um nenúfar |
Para um conjunto de casos de teste valendo 60% dos pontos, o número N de nenúfares será menor ou igual a 10.
3 2 8 7 10 1 6 2 5 3 4 2 2 4 1 5 5 6 6 6 4 7 5 6 2
6 1