

Só existem dois tipos de programadores: os que colocam as chavetas na mesma linha de outras instruções (compactos) e os que colocam as chavetas numa linha separada (separatistas).
Sendo o responsável pelos recursos humanos de uma startup não podes ignorar este problema! Estás encarregue de contratar N programadores, C deles de estilo de código compactos e S de estilo separatista. As posições onde eles vão ficar colocados estão numeradas de 0 a (N)-1 e os fundadores da empresa entregaram-te um esquema descrevendo a hierarquia de funcionamento desejada. Esta hierarquia tem a forma de uma árvore, ou seja, todos os programadores excepto um (o líder, na raíz que é sempre na posição zero) respondem directamente a um e só um programador. A figura seguinte ilustra algumas possíveis árvores:
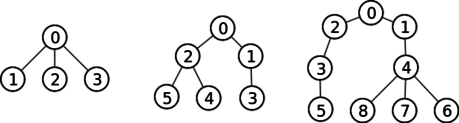
Uma vez que os fundadores da empresa estão em polos opostos no estilo de código, tens de encontrar uma alocação dos programadores à árvore que maximize a variedade, de modo a agradar a ambos. Podes optar por colocar em cada posição (nó da árvore) um compacto (azul) ou um separatista (vermelho), desde que no final tenhas exactamente o número pedido de cada tipo. O valor da variedade de um nó i é igual ao número de programadores de tipo diferente desse nó na sub-árvore com raíz nessa posição. A variedade total de uma árvore é simplesmente a soma da variedade de todas as suas posições.
Como exemplo, a tabela seguinte ilustra a variedade de três das muitas alocações possíveis de programadores a uma hierarquia sabendo que temos de usar 4 compactos e 2 separatistas:
| Árvore | Variedade do nó | Variedade Total |
|||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
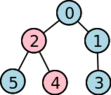 |
2 | 0 | 1 | 0 | 0 | 0 | 3 |
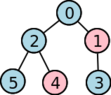 |
2 | 1 | 1 | 0 | 0 | 0 | 4 |
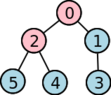 |
4 | 0 | 2 | 0 | 0 | 0 | 6 |
Tens de ajudar a descobrir a melhor alocação de programadores!
Dada uma árvore descrevendo a hierarquia de N posições, e um conjunto de P pares de números Ci e Si, a tua tarefa é descobrir, para cada par, qual a maior variedade possível de obter numa árvore à qual foram alocados Ci compactos e Si separatistas.
A primeira linha contém um inteiro N indicando o número de posições na hierarquia em forma de árvore. Seguem-se N-1 linhas, cada uma no formato A B indicando que o nó B responde directamente ao nó A.
A linha seguinte contém um inteiro P indicando o número de perguntas. Seguem-se P linhas, cada uma no formato Ci Si, indicando que queremos saber a melhor colocação para Ci compactos e Si separatistas.
O output é constituído por P linhas, cada um com um único inteiro Ri, a resposta para a pergunta i, ou seja, qual a maior variedade possível de obter ao colocar na árvore Ci compactos e Si separatistas.
São garantidos os seguintes limites em todos os casos de teste:
| 2 ≤ N ≤ 100 | Número de programadores a contratar | |
| 1 ≤ P ≤ 10 | Número de perguntas | |
| Ci + Si = N | Número de compactos e separatistas em cada pergunta |
Para um conjunto de casos de teste valendo 20% dos pontos, acontece sempre que N≤5.
Para um conjunto de casos de teste valendo 50% dos pontos, acontece sempre que N≤25.
6 0 1 0 2 2 4 2 5 1 3 2 4 2 1 5
6 5
A árvore é a da tabela no enunciado. O primeiro caso, 4 compactos e 2 separatistas, é precisamente o da tabela e é possível obter árvore com variedade 6 (tal como ilustrado). O segundo caso tem apenas um compacto e 5 separatistas e o melhor que é possível obter é uma árvore com variedade 5 (com o compacto a ficar na raíz da árvore).
4 0 1 0 2 0 3 5 0 4 1 3 2 2 3 1 4 0
0 3 2 3 0