Problema B - Depois da prova

Depois de todas as qualificações, finais, seleções e tudo mais, é hora de relaxar e premiar o grande esforço dedicado a cada prova. Para tal, nada melhor que um bom jogo de bowling olímpico.

O bowling olímpico é uma modalidade que consiste em derrubar N pinos dispostos numa linha. Cada pino i tem uma altura h_i e encontra-se numa posição x_i.

Neste jogo o objetivo é atirar bolas contra os pinos de maneira a fazê-los tombar. Quando uma bola acerta num pino ele tomba para um dos lados, ou para a esquerda, ou para a direita. Ao cair, o pino i derruba todos os pinos que estejam a uma distância menor ou igual a h_i para o lado que tombou. Estes por sua vez são derrubados para o mesmo lado e derrubam todos os que estão ao seu alcance e por ai fora até à queda em cadeia terminar. É assumido que os pinos não têm largura, são como segmentos de reta.

Cada jogador pode atirar as bolas que quiser para os pinos que quiser. Além disso, é muito fácil orientar a bola de maneira a fazer um pino cair para o lado pretendido, por isso podemos assumir que cada jogador numa jogada escolhe um pino que ainda não tenha sido tombado e um sentido, e atira uma bola de modo a derrubar esse pino para o sentido escolhido.

O objetivo do jogo é simplesmente derrubar todos os pinos e ganha quem o fizer usando menos bolas. Consegues calcular o número mínimo de bolas a usar para derrubar todos os pinos?

Por exemplo, imaginem que temos N = 8 pinos, como mostra a imagem seguinte.

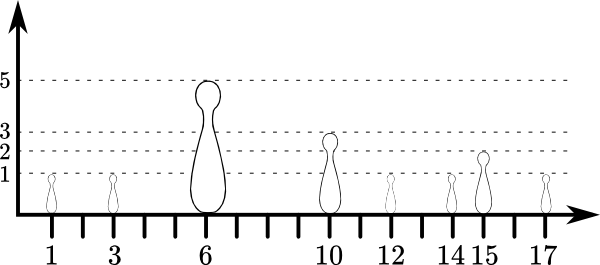
Neste caso conseguimos derrubar todos os pinos com apenas 3 bolas:

• Lançamos uma bola que derruba o pino na posição 6 fazendo o tombar para a esquerda, no processo ele derruba ainda os pinos nas posições 1 e 3;
• Lançamos uma bola que derruba o pino na posição 10 fazendo o tombar para a direita, no processo ele derruba ainda o pino na posição 12;
• Lançamos uma bola que derruba o pino na posição 14 fazendo o tombar para a direita, no processo ele derruba ainda o pino na posição 15 que por sua vez cai para a direita e derruba o pino na posição 17;

O Problema

Dado um conjunto de N pinos, a altura h_i e posição x_i de cada um, calcular o mínimo número de bolas necessárias para derrubar todos os pinos.

Input

Na primeira linha vem um inteiro, N que representa o número de pinos.

Segue-se uma linha com N inteiros, sendo que o i-ésimo inteiro representa a posição x_i do i-ésimo pino. NOTA: é garantido que não há dois pinos na mesma posição.

Segue-se uma linha com N inteiros, sendo que o i-ésimo inteiro representa a altura h_i do i-ésimo pino.

Output

O output contém apenas um inteiro, que representa o menor número de bolas necessárias para derrubar todos os pinos.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

Os casos de teste deste problema estão organizados em 5 grupos com restrições adicionais diferentes:

Input do Exemplo 1

8
3 10 1 6 14 17 15 12
1 3 1 5 1 1 2 1

Output do Exemplo 1

3

Explicação do Exemplo 1

Este exemplo corresponde ao mencionado no enunciado.

Input do Exemplo 2

13
10 15 2 5 9 23 30 4 33 22 26 19 12
3 4 1 6 4 2 3 3 1 4 3 1 2

Output do Exemplo 2

3