
O pequeno Henrique foi visitar o novo Parque de dinossauros no Porto com a sua família enquanto o seu irmão participava nas ONI. Após muito passear já tinha visto quase tudo, até que encontrou o assustador Tiranossauro. Ficou tão assustado que quis fugir para o sítio de interesse do parque mais afastado possível. No entanto o mapa parecia muito complexo para ele descobrir para onde ir.
O mapa está organizado em pontos de interesse, por onde o Henrique pode passar, e ligações (pequenas estradas) de comprimento igual. Após analisar com muito cuidado, chegou à conclusão que entre quaisquer dois pontos de interesse existe no mínimo um e no máximo dois caminhos simples. Isto é, para ir de um ponto para o outro, no máximo, existem dois caminhos que diferem em pelo menos um ponto e não repetem pontos, e no mínimo um nas mesmas condições. Ainda mais, entre dois pontos existe no máximo uma estrada (uma ligação direta).
Além disso, o parque tem vários dinossauros que assustam o Henrique e por isso para cada um precisa de saber para onde deve fugir. Ou seja, para cada ponto com um dinossauro assustador o Henrique quer saber quanto tem de andar para chegar ao ponto de interesse mais afastado desse ponto, ou seja, qual a distância entre o ponto atual e o ponto mais afastado desse ponto atual. A distância entre dois pontos de interesse é dada pelo menor número de ligações para ir de um ponto ou outro. Nota também que os dinossauros estão todos em pontos de interesse.
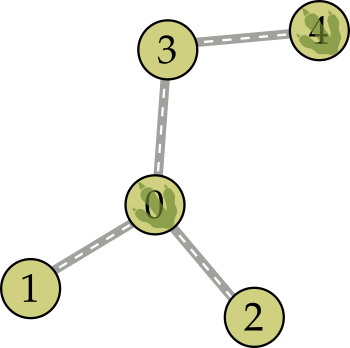
Considera por exemplo o seguinte mapa:

Há dois pontos de interesse com dinossauros. O ponto 4, do qual os pontos mais distantes são o 1 e 2, e logo a resposta é 3, a distância a que estes dois se encontram. De seguida, o ponto 0, do qual o ponto mais distante é o 4, logo a resposta para este caso seria 2.
Sabendo isto, e dado o mapa, será que consegues ajudar o pequeno Henrique a esconder-se e dizer-lhe a que distância está o ponto mais afastado de cada ponto onde ele se possa assustar? Nota que o Henrique quer chegar ao ponto o mais rápido possível, por isso a distância é percorrendo o menor caminho que existe.
Dado o número N de pontos de interesse numerados de 0 a N - 1, o número L de ligações entre eles por onde o Henrique pode passar, responder a Q perguntas de qual a distância do ponto mais afastado do ponto Qi.
Na primeira linha vêm três inteiros, o primeiro representando o número N de pontos de interesse, o segundo o número L de ligações e o terceiro o número Q de perguntas.
Seguem-se L linhas, onde a i-ésima tem um par Ai Bi, que representam uma ligação bidirecional entre Ai e Bi.
Finalmente, vêm Q linhas, cada uma com um inteiro Qi indicando o ponto de interesse da i-ésima pergunta (um número entre 0 e N-1).
O output deve conter Q linhas com a reposta a cada uma das perguntas.
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| N ≤ 100 000 | Número de pontos | |
| L ≤ 500 000 | Número de ligações | |
| Q ≤ 100 000 | Número de perguntas |
Os casos de teste deste problema estão organizados em 5 grupos com restrições adicionais diferentes:
| Grupo | Número de Pontos | Restrições adicionais |
|---|---|---|
| 1 | 20 | N ≤ 1000, L ≤ 5000 e Q ≤ 1000 |
| 2 | 25 | Há exatamente um caminho entre cada ponto |
| 3 | 5 | Há exatamente dois caminhos entre cada ponto |
| 4 | 20 | Há um conjunto de três pontos ligados dois a dois |
| 5 | 30 | - |
5 4 2 4 3 3 0 0 2 1 0 4 0
3 2
8 8 5 7 6 4 2 3 1 4 5 2 3 0 6 7 2 3 7 3 7 4 5 4
3 3 4 5 4