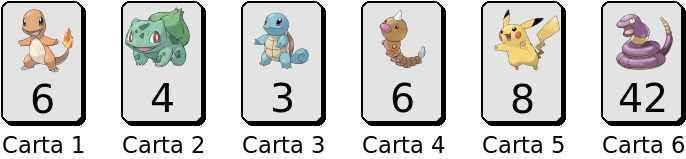

O Vicente tem N cartas de Pokémon que todos os dias coloca em fila numa mesa durante o intervalo da escola. As cartas são numeradas de 1 até N e cada carta contém um número inteiro indicando a energia do Pokémon correspondente. Por exemplo, poderia ter as seguintes N=6 cartas:

Todos os dias o Simão traz também as suas cartas e quer fazer um combate com o Vicente. O Simão escolhe uma sequência contígua de cartas do Vicente, expressas através de dois inteiros a e b que indicam a posição inicial e final da sequência a considerar. Por exemplo, uma escolha com a=1 e b=3 para a figura anterior indicaria as cartas com energias 6, 4 e 3.
Para o combate, o Vicente pode escolher um qualquer par de cartas da sequência escolhida. Para a=1 e b=3 os pares possíveis seriam as cartas (1,2), (1,3) ou (2,3).
O critério que ele usa é escolher o par com o maior máximo de energia (que será o pokémon que ele usa preferencialmente para a luta). Se escolher duas cartas com energia c1 e c2, isto daria um valor de maximo(c1,c2) se a energia das cartas for diferente. Se por acaso ambas as cartas tiverem a mesma energia (ou seja, c1=c2), então o valor delas é c1+1 (pois nesse caso ambas as cartas são boas para lutar e é um par melhor que só ter uma das cartas com o maior valor).
O Vicente quer mesmo saber qual é o par de cartas da sequência que deve escolher para maximizar o seu valor, seja qual for a escolha do Simão. Será que podes ajudá-lo? Por exemplo, para a=1 e b=3 o melhor valor de um par é 6, e pode ser obtido com os pares de energia (6,4) ou (6,3). Já se a sequência fosse a=1 e b=4 o melhor valor seria 7, que pode ser obtido com o par (6,6).
Dada uma sequência de N cartas, indicadas pela sua energia, e S escolhas de sequência do Simão (cada uma indicada pela posição inicial e final), a tua tarefa é indicar, para cada escolha, qual o maior valor de um par de cartas da sequência correspondente.
A primeira linha contém dois inteiros N S, indicando respetivamente o número de cartas do Vicente e o número de escolhas de sequência do Simão.
A segunda linha contém N inteiros c1, c2, ..., cN, indicando as energias de todas as cartas na ordem em que estão na fila.
Seguem-se S linhas indicando as sequências que o Simão escolhe. Cada uma destas linhas contém dos inteiros a b indicando respetivamente a posição inicial e final da sequência, sendo garantido que a sequência tem tamanho maior ou igual a dois.
O output deve conter S linhas, uma por cada sequência, na mesma ordem do input. Em cada linha deve vir um único inteiro indicando o maior valor de um par de cartas escolhido dentro da sequência correspondente.
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| 2 ≤ N ≤ 100 000 | Número de cartas do Vicente | |
| 1 ≤ S ≤ 100 000 | Número de escolhas de sequências do Simão | |
| 1 ≤ a < b ≤ N | Posições inicial e final de cada sequência | |
| 1 ≤ ci ≤ 1 000 000 | Energia de cada carta |
Os casos de teste deste problema estão organizados em 4 grupos com restrições adicionais diferentes:
| Grupo | Número de Pontos | Restrições adicionais |
|---|---|---|
| 1 | 10 | N ≤ 100, S ≤ 100, ci ≤ 10 000 |
| 2 | 25 | N ≤ 2 000, S ≤ 2 000, ci ≤ 10 000 |
| 3 | 30 | ci ≤ 2 |
| 4 | 35 | - |
6 5 6 4 3 6 8 42 1 3 1 4 2 3 3 5 1 6
6 7 4 8 42