Problema B - No Fundo do Mar
 O Vladimir
está a aprender mergulho em apneia (sem garrafa de oxigénio). Um dos seus exercícios é
deixar cair um objeto, esperar que ele lentamente chegue ao fundo
do mar e depois mergulhar para apanhá-lo. O Vladimir pôs-se a
pensar que se conhecesse com algum pormenor o fundo do mar,
poderia determinar a altura mais profunda onde o objeto pode
cair, e com isso estimar o tempo máximo em qu tem de suster a
respiração.
O Vladimir
está a aprender mergulho em apneia (sem garrafa de oxigénio). Um dos seus exercícios é
deixar cair um objeto, esperar que ele lentamente chegue ao fundo
do mar e depois mergulhar para apanhá-lo. O Vladimir pôs-se a
pensar que se conhecesse com algum pormenor o fundo do mar,
poderia determinar a altura mais profunda onde o objeto pode
cair, e com isso estimar o tempo máximo em qu tem de suster a
respiração.
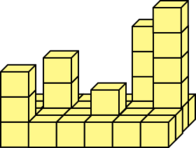
O fundo do mar pode ser modelado como uma matriz onde cada
posição tem um número inteiro representando a sua altitude. A
figura seguinte ilustra um possível fundo com 4 linhas e 6
colunas e a respetiva matriz de altitudes:
|
|
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
O objeto que é atirado ao fundo do mar pode ser modelado
como um retângulo que cai sempre na mesma orientação, com os
seus lados paralelos aos lados da matriz (sem admitir
rotações). O objeto é rígido e mal encontra um obstáculo fica
imóvel, parando de descer. Sabemos portanto que quando um
retângulo cai, fica imobilizado no ponto de maior altitude da
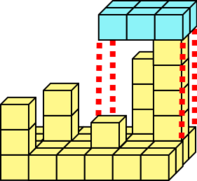
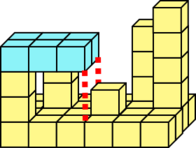
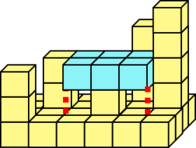
área que cobre. As figuras seguintes ilustram 3 possíveis sítios
onde um retângulo de 2 linhas por 3 colunas podia cair no fundo
do mar mostrado anteriormente, ilustrando em que altura ficava
imobilizado em cada caso (igual a um mais a máxima altitude da área correspondente):
 |
|
 |
|
 |
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
|
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
|
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
| Altura = 5 |
|
Altura = 3 |
|
Altura = 2 |
Quando está à superfície, o Vladimir não consegue ver o fundo do
mar, e por isso não sabe em que posição exata vai atirar o
retângulo. O que ele gostava mesmo de saber era qual a profundidade
máxima (ou seja, a altura mínima) onde o objeto pode cair. Para o
caso atrás ilustrado, o pior caso possível é precisamente o de
altura 2. Todas os outros sítios onde o retângulo pode cair dariam
origem a uma altura maior ou igual a 2. Tens de ajudar o Vladimir!
Sabendo as dimensões de alguns objetos que ele costuma atirar ao
mar, até onde pode cair cada um deles?
O Problema
Dada um matriz de L linhas por C colunas com
inteiros representando as altitudes de cada ponto do fundo do
mar, e um conjunto de R retângulos, a tua tarefa é
descobrir para cada um deles qual a altura mínima onde podem
ficar imobilizados.
Input
Na primeira linha vêm dois inteiros L e C,
indicando o número de linhas e colunas da matriz de altitudes do
fundo do mar. Seguem-se L linhas, cada uma com C
inteiros Aij representando a matriz em si.
Depois de matriz vem uma linha com um único inteiro R
representando o número de diferentes retângulos a
considerar. Seguem-se R linhas, cada uma com dois
inteiros RLi e RCi
representando respetivamente o número de linhas e colunas do
retângulo.
Output
O output deve conter R linhas, uma para cada retângulo,
contendo um inteiro indicando a altura mínima onde podem cair, como atrás explicado.
Restrições
São garantidos os seguintes limites em todos os casos de teste que
irão ser colocados ao programa:
| 1 ≤ L, C ≤ 900 |
|
Número de linhas e colunas do fundo do mar |
| 0 ≤ Aij ≤ 106 |
|
Altura de cada posição do fundo do mar |
| 1 ≤ R ≤ 10 |
|
Número de retângulos |
| 1 ≤ RLi ≤ L, 1 ≤ RCi ≤ C |
|
Dimensões dos retângulos a considerar |
Os casos de teste deste problema estão organizados em 4 grupos
com restrições adicionais diferentes:
| Grupo |
Nº de Pontos |
Restrições adicionais |
| 1 |
25 |
L, C ≤ 20, Aij ≤ 100 |
| 2 |
25 |
L, C ≤ 200 |
| 3 |
25 |
L, C ≤ 600 |
| 4 |
25 |
(nenhuma restrição adicional) |
Exemplo de Input 1
4 6
0 0 0 0 3 0
0 2 0 0 0 4
0 0 0 1 0 0
2 0 0 0 0 0
4
2 3
1 4
2 4
4 5
Exemplo de Output 1
2
1
2
4
Explicação do Exemplo 1
A figura seguinte ilustra cada um dos 4 retângulos dados, indicando uma posição possível onde é atingida a altura mínima.
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
|
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
|
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
|
| 0 | 0 | 0 | 0 | 3 | 0 |
| 0 | 2 | 0 | 0 | 0 | 4 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
|
| Altura = 2 |
|
Altura = 1 |
|
Altura = 2 |
|
Altura = 4 |
| [retângulo 2x3] |
|
[retângulo 1x4] |
|
[retângulo 2x4] |
|
[retângulo 4x5] |
Exemplo de Input 2
5 8
53 70 57 97 32 36 23 39
81 44 65 66 80 51 78 67
32 42 22 9 80 20 53 37
74 95 82 8 78 9 9 83
31 18 80 63 54 4 54 87
3
2 3
3 2
2 4
Exemplo de Output 2
67
55
79
Explicação do Exemplo 2
A figura seguinte ilustra cada um dos 3 retângulos dados, indicando uma posição possível onde é atingida a altura mínima.
| 53 |
70 |
57 |
97 |
32 |
36 |
23 |
39 |
| 81 |
44 |
65 |
66 |
80 |
51 |
78 |
67 |
| 32 |
42 |
22 |
9 |
80 |
20 |
53 |
37 |
| 74 |
95 |
82 |
8 |
78 |
9 |
9 |
83 |
| 31 |
18 |
80 |
63 |
54 |
4 |
54 |
87 |
|
|
| 53 |
70 |
57 |
97 |
32 |
36 |
23 |
39 |
| 81 |
44 |
65 |
66 |
80 |
51 |
78 |
67 |
| 32 |
42 |
22 |
9 |
80 |
20 |
53 |
37 |
| 74 |
95 |
82 |
8 |
78 |
9 |
9 |
83 |
| 31 |
18 |
80 |
63 |
54 |
4 |
54 |
87 |
|
|
| 53 |
70 |
57 |
97 |
32 |
36 |
23 |
39 |
| 81 |
44 |
65 |
66 |
80 |
51 |
78 |
67 |
| 32 |
42 |
22 |
9 |
80 |
20 |
53 |
37 |
| 74 |
95 |
82 |
8 |
78 |
9 |
9 |
83 |
| 31 |
18 |
80 |
63 |
54 |
4 |
54 |
87 |
|
| Altura = 67 |
|
Altura = 55 |
|
Altura = 79 |
| [retângulo 2x3] |
|
[retângulo 3x2] |
|
[retângulo 2x4] |
Final Nacional das ONI'2016
Departamento de Ciência de Computadores
Faculdade de Ciências da Universidade do Porto
(22 de Abril de 2016)
 O Vladimir
está a aprender mergulho em apneia (sem garrafa de oxigénio). Um dos seus exercícios é
deixar cair um objeto, esperar que ele lentamente chegue ao fundo
do mar e depois mergulhar para apanhá-lo. O Vladimir pôs-se a
pensar que se conhecesse com algum pormenor o fundo do mar,
poderia determinar a altura mais profunda onde o objeto pode
cair, e com isso estimar o tempo máximo em qu tem de suster a
respiração.
O Vladimir
está a aprender mergulho em apneia (sem garrafa de oxigénio). Um dos seus exercícios é
deixar cair um objeto, esperar que ele lentamente chegue ao fundo
do mar e depois mergulhar para apanhá-lo. O Vladimir pôs-se a
pensar que se conhecesse com algum pormenor o fundo do mar,
poderia determinar a altura mais profunda onde o objeto pode
cair, e com isso estimar o tempo máximo em qu tem de suster a
respiração.


