Problema C - Harmonia entre Nações

Após uma longa guerra entre a Nação do Fogo e o Reino da Terra, vivem-se agora tempos de paz entre todas as nações. É o dever do Avatar manter este clima pacífico e para isso conta com a ajuda do mundo dos espíritos.

Para garantir a harmonia o Avatar tem de ter em conta as relações de confiança entre todos os habitantes do planeta. Estas relações são representadas por um grafo dirigido onde uma aresta de A para B simboliza que o habitante A confia no habitante B. A figura seguinte ilustra um possível grafo com habitantes numerados de 1 a 13. Nesse grafo, por exemplo, é possível verificar que 1 confia em 2, 4 confia em 5 e 7 e 12 não confia em ninguém.

Um grupo de habitantes diz-se "pacífico" se satisfizer a seguinte propriedade: se A e B pertencerem ao grupo então existe um caminho de A para B ou de B para A no grafo. Por exemplo, na figura de cima, o grupo constituído pelos habitantes {1,2,3,4,5,7,8} é pacífico. Outros grupos que satisfazem esta propriedade são por exemplo o {12}, {9,10,12} ou {1,2,3,4,5,6}.

De maneira a guiar o Avatar na sua tarefa de manter a harmonia, o espirito guardião descobriu que é necessário ter em conta o "grau de harmonia", que é definido como o tamanho do maior grupo pacifico de habitantes. Para o exemplo de cima, este valor é precisamente sete (número de habitantes no grupo {1,2,3,4,5,7,8}), pois todos os outros possíveis grupos pacíficos têm um tamanho inferior.

O Avatar precisa agora de calcular o grau de harmonia para saber se a paz em que se vive será duradora mas, infelizmente, existem imensos habitantes e ele está com muitas dificuldades. Será que podes ajudá-lo a resolver este problema antes que uma nova guerra comece?

O Problema

Dado um grafo de relações de confiança como atrás definido, a tua tarefa é determinar o tamanho do maior grupo pacífico, ou seja, o tamanho do maior grupo de nós do grafo tal que se A e B pertencem ao grupo, então existe um caminho de A para B ou de B para A.

Input

Na primeira linha é dado um inteiro, G, indicando o grupo de casos de teste (vê os detalhes de cada grupo na secção "Restrições"). Na segunda linha vêm dois inteiros, N e M, indicando o número de habitantes e o número de relações diretas de confiança, respetivamente. Seguem-se M linhas, cada uma contendo dois inteiros, A_i e B_i, significando que A_i confia em B_i. Os habitantes estão numerados de 1 a N.

Output

O output deve conter apenas uma linha com um inteiro, o grau de harmonia, ou seja, o tamanho do maior grupo pacífico.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

Os casos de teste deste problema estão organizados em 5 grupos com restrições adicionais diferentes:

Exemplo de Input 1

1
8 10
1 2
2 1
4 5
5 6
5 4
6 7
6 8
8 6
7 6
6 5
    

Exemplo de Output 1

5
    

Explicação do Exemplo 1

Exemplo de Input 2

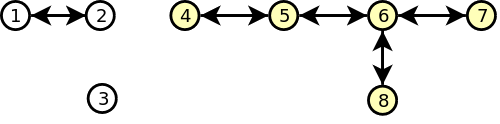
2
8 6
1 2
2 3
2 4
4 5
6 7
8 4
    

Exemplo de Output 2

4
    

Explicação do Exemplo 2

Exemplo de Input 3

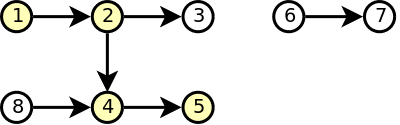
3
7 6
1 2
2 3
3 4
4 2
5 6
6 7
    

Exemplo de Output 3

4
    

Explicação do Exemplo 3

Exemplo de Input 4

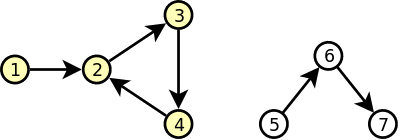
4
13 12
1 2
2 3
3 4
4 5
5 4
5 3
4 7
7 8
5 6
9 10
10 11
10 12
    

Exemplo de Output 4

7
    

Explicação do Exemplo 4

(Exemplo explicado no enunciado do problema)