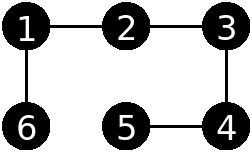

Nos concursos de programação universitários os concorrentes participam em grupos de exatamente três concorrentes. Na Universidade das ONI há N alunos que querem competir em concursos de programação, onde N é um múltiplo de 3, sendo que os alunos são identificados por inteiros consecutivos entre 1 e N.
Infelizmente, existem exatamente N-1 conflitos entre alunos, formando aquilo que pode ser visto como um grafo de conflitos, onde existe uma ligação entre um par de alunos (a,b) se esses dois alunos têm um conflito. Sabe-se que este grafo é conexo (ou seja, há um caminho entre qualquer par de alunos) e não contém qualquer ciclo (um caminho que começa e termina no mesmo aluno).
Podemos por exemplo ter 6 alunos e os seguintes conflitos: (2,1), (2,3), (4,3), (4,5) e (6,1), que formariam o grafo da figura seguinte:
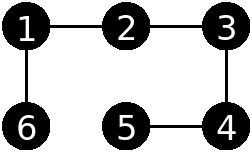
Queremos formar equipas de exatamente 3 elementos de forma a que cada aluno esteja em exatamente uma equipa e que não haja qualquer conflito entre membros de uma equipa. Para o exemplo da figura anterior, poderíamos por exemplo formar duas equipas: uma com os alunos 1 3 5 e outra com os alunos 2 4 6.
Dados N - 1 conflitos, determina se é possível formar equipas que satisfazem esta condição e se sim indica uma possível distribuição de equipas.
A primeira linha contém um inteiro N, representando o número de alunos.
Seguem-se N - 1 linhas, cada uma contendo um par de inteiros diferentes (a,b) separados por espaços, representando cada conflito. O mesmo par nunca aparece duas vezes no input.
Se não for possível formar equipas o output deve conter apenas o inteiro -1.
Caso contrário o output deve conter primeiro uma linha com o inteiro 1. Devem seguir-se N / 3 linhas cada uma com 3 inteiros entre 1 e N separados por espaços, onde cada linha representa uma equipa.
Nota: quando há várias respostas possíveis, podes imprimir qualquer uma.
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| 3 ≤ N ≤ 100 000 | Número de alunos | |
| 1 ≤ a, b ≤ N | Índices dos alunos de um par em conflito |
Nota: N será sempre um múltiplo de 3.
Os casos de teste deste problema estão organizados em 4 grupos com restrições adicionais diferentes:
| Grupo | Número de Pontos | Restrições adicionais |
|---|---|---|
| 1 | 15 | N ≤ 9 |
| 2 | 25 | N ≤ 100 |
| 3 | 25 | O grafo de conflitos é uma linha |
| 4 | 35 | - |
6 2 1 2 3 4 3 4 5 6 1
1 1 3 5 2 4 6
6 2 1 2 3 4 3 1 5 3 6
-1
12 1 2 3 2 3 4 5 1 1 6 7 5 8 5 9 6 10 8 11 6 12 9
1 1 3 7 2 4 5 6 10 12 8 9 11