
As ONI estão a desenvolver um carro automático. Para testar o carro as ONI têm uma grelha quadrada de N por N onde o carro se movimenta entre células. Quando o carro está numa célula (x, y) só se pode movimentar para as células (x + 1, y) e (x, y + 1). Adicionalmente, há K células inacessíveis, sobre as quais o carro não pode estar. É garantido que as células (1, 1) e (N, N) são sempre acessíveis.
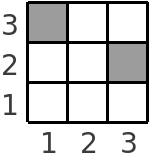
A figura seguinte ilustra um exemplo de uma grelha de 3 por 3 com duas células inacessíveis:

Para testar o carro é importante saber o número de caminhos distintos que o carro pode fazer começando na célula (1, 1) e terminando na célula (N, N) que evitam as K células inacessíveis. Como o número de caminhos pode ser muito grande, deves calcular a resposta módulo 109 + 7.
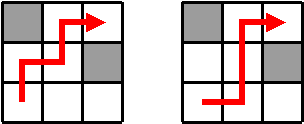
Para o exemplo da figura anterior existem dois caminhos distintos:
Dadas as dimensões N de uma grelha e um conjunto de K células inacessíveis, calcula o número de caminhos distintos de (1, 1) até a (N, N) módulo 109 + 7.
A primeira linha contém dois inteiros separados por espaços N, representando o tamanho da grelha, e K, representando o número de células inacessiveis.
Seguem-se K linhas, cada uma contendo um par de inteiros representando a coluna e linha de cada célula inacessível. Todas as células indicadas são válidas e nunca existem células repetidas.
O output deve conter um inteiro representando o número de caminhos módulo 109 + 7.
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| 1 ≤ N ≤ 100 000 | Tamanho da grelha quadrada | |
| 1 ≤ K ≤ 1 000 | Número de células inacessíveis |
Os casos de teste desta parte do problema estão organizados em 4 grupos com restrições adicionais diferentes:
| Grupo | Número de Pontos | Restrições adicionais |
|---|---|---|
| 1 | 15 | N ≤ 20, K ≤ 20 |
| 2 | 25 | N ≤ 2 000 |
| 3 | 25 | K = 1 |
| 4 | 35 |
O operador módulo em C++ é o símbolo %. Algumas propriedades importantes sobre este operador que podem ser úteis para a vossa solução:
(a + b) % n é igual a ((a % n) + (b % n)) % n(a - b) % n é igual a ((a % n) - (b % n) + n) % n(a * b) % n é igual a ((a % n) * (b % n)) % n
Uma outra fórmula que pode ser útil é a fórmula de inverso
modular. Esta fórmula só se aplica se n for um
número primo, mas notem que 109 + 7 é primo. Na
fórmula em baixo ^ significa exponenciação:
(a^(-1)) % n é igual a (a^(n - 2)) % n3 2 3 2 1 3
2
5 4 1 2 5 2 1 4 3 4
19
10 5 1 6 2 8 3 2 1 10 10 2
28368