Bases de Dados (CC2005), Dep. Ciência de Computadores, FCUP
Eduardo R. B. Marques, DCC/FCUP

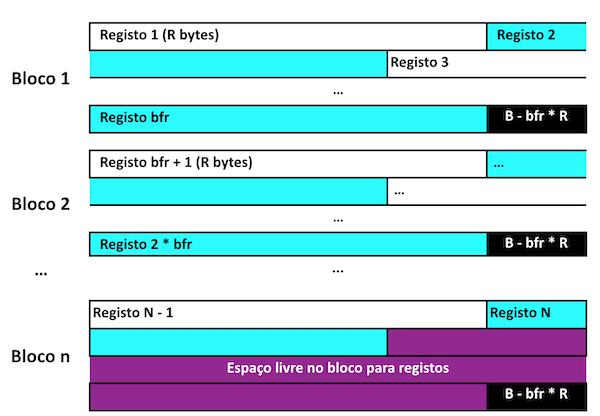
\( B = 4096 \)
\(T_1: \quad N = 10,000 \quad R = 32 \)
\(T_2: \quad N = 100,000 \quad R = 130 \)
\(T_1: \quad bfr = \lfloor 4096/32 \rfloor = 128 \quad B - bfr * R = 0 \quad n = \lceil 10000 \:/\: 128 \rceil = 79 \)
\(T_2: \quad bfr = \lfloor 4096/130\rfloor = 31 \quad B - bfr * R = 66 \quad n = \lceil 100000 \:/\: 31 \rceil = 3226 \)
Para \(T_1\): \( \lceil log_2(79) \rceil = 7\) pela chave primária, por outro atributo \(n = 79\).
Para \(T_2\): \( \lceil log_2(3226) \rceil = 12\) pela chave primária, por outro atributo \(n = 3226\).
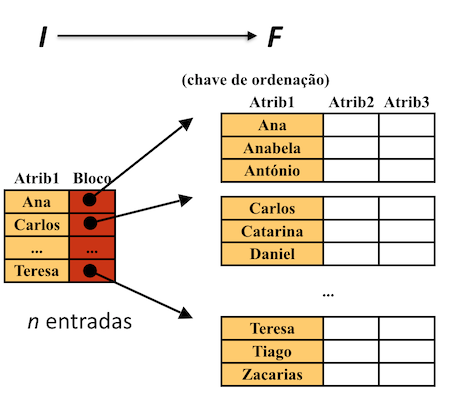
Para \(T_1\):
\(
N_I = n = 100 \quad
R_I = 4 + 8 = 12 \quad
bfr_I = \lfloor 4096 / 12\rfloor = 341 \quad
n_I = \lceil 100 / 341 \rceil = 1
\)
portanto precisamos de apenas \(2=1+1\) acessos a disco, um para consulta do índice e outro para o bloco do ficheiro. Seriam \(\lceil log_2(100) \rceil = 7\) se o índice não estivesse definido.
Para \(T_2\):
\(
N_I = n = 10000 \quad
R_I = 12 + 8 = 20 \quad
bfr_I = \lfloor 4096 / 20\rfloor = 204 \quad
n_I = \lceil 10000 / 204 \rceil = 50
\)
portanto precisamos de \(7=\lceil log_2(50)\rceil+1\) acessos a disco no máximo. Seriam \(\lceil log_2(10000) \rceil = 14\) se o índice não estivesse definido.
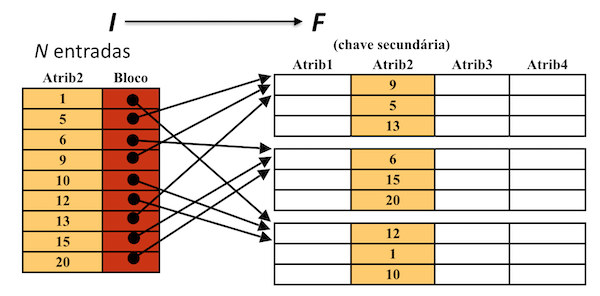
Temos
\( N_I = N = 25000 \quad R_I = 8 + 8 = 16 \quad bfr_I = \lfloor 4096 / 16\rfloor = 256 \quad n_I = \lceil 25000 / 256 \rceil = 98 \)
portanto precisamos de \(8=\lceil log_2(98)\rceil +1\) acessos a disco no máximo vs. \(n=400\) numa pesquisa linear usando a chave secundária.
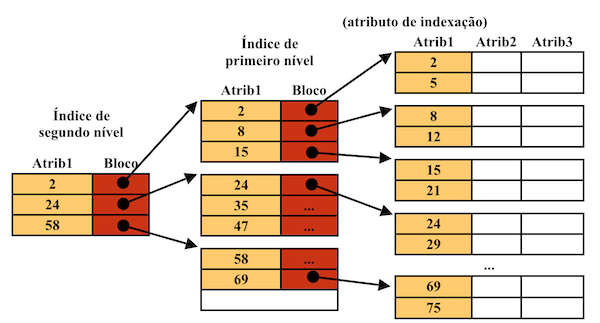
No segundo nível teríamos
\( N_{I}^2 = n_I = 98 \quad R_I^2 = R_I = 16 \quad bfr_I^2 = bfr_I = 256 \quad n_I^2 = \lceil 98 / 256 \rceil = 1 \)
Portanto precisávamos só de um bloco extra em disco. Quanto a acessos a disco seriam sempre \(3 = 1 + 1 + 1\) (índice de 2º nível, índice de 1º nível, ficheiro).
Não faz sentido um índice de 3º nível porque o índice de 2º nível cabe todo em 1 bloco de disco.