Assignment I: All-Pairs Shortest Path Problem
Goal
Allow students to acquire sensibility and practical experience with
parallel programming for distributed memory environments using the MPI
framework.
Description
The problem to be solved consists in determining all shortest paths
between pairs of nodes in a given graph. This is the well
known all-pairs shortest path problem.
The idea is simple: given a directed graph G = (V,E) in which V is the
set of nodes (or vertices) and E is the set of links (or edges)
between nodes, the goal is to determine for each pair of nodes (vi,vj)
the size of the shortest path that begins in vi and ends in vj. A path
is simply a sequence of links in which the end node and start node of
two consecutive links are the same. One link can be seen as a tuple of
the form <vi, vj, t> where vi is the origin node, vj is the
destination node and t is the size of the link between the nodes. The
sum of the sizes of the links is the size of the path between vi and
vj.
Implementation
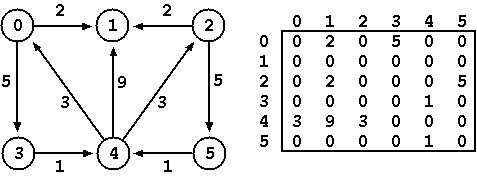
A directed graph with V nodes can be represented as a matrix D1 with
dimension NxN (N = 6 for the example that follows) where each element
(i,j) of the matrix represents the size of the link that connects node
vi with node vj. A zero value means that there is no connection
between the two nodes.
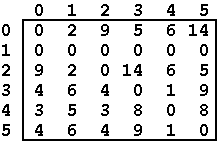
The solution of the problem may also be represented by a matrix Df
with dimension NxN where each element (i,j) of the matrix corresponds
to the size of the shortest path among all possible paths between
nodes vi and vj.
Min-plus matrix multiplication, also known as Distance Product, is an
adapted form of matrix multiplication in which the multiplication and
sum operations are replaced by operations of sum and minimum,
respectively. Using this min-plus matrix multiplication strategy, the
Repeated Squaring algorithm allows one to obtain the matrix Df from
matrix D1 by building successively matrices D2 = D1xD1, D4 = D2xD2, D8
= D4xD4, ..., until Df = DgxDg, with f >= N and g < N
(see here
a more detailed explanation of this algorithm).
A well-known algorithm to efficiently compute the multiplication of
matrices with the same size in distributed environments is Fox's
algorithm. The application of Fox's algorithm is not always possible,
it depends on the dimension of the matrices being multiplied and on
the available processes. Given matrices of size NxN and P processors,
there must exist an integer Q such that P = Q*Q and N mod Q = 0,
otherwise the algorithm cannot be applied. Fox's algorithm then
divides the NxN matrices into sub-matrices with dimension (N/Q)x(N/Q)
and assigns each one to the P processors available in the system.
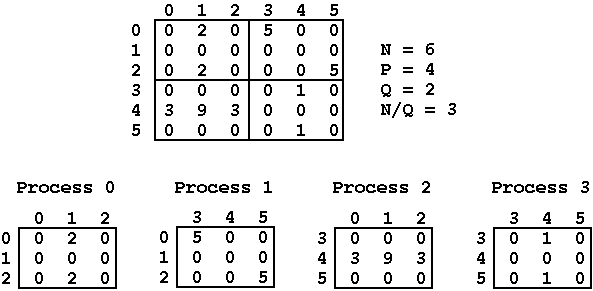
To compute the result of each sub-matrix multiplication, each process
only needs to exchange information with the processes in the same row
and same column of its sub-matrix, thus reducing the number of
messages that need to be exchanged (see pages 29 and 30 of
the A Users' Guide to
MPI for a more detailed explanation of Fox's
algorithm). Applying successively the Fox algorithm allows one to
calculate matrices D2, D4, ..., Df of the Repeated Squaring algorithm
and thus obtain the matrix that is the solution to our problem.
Input and Output
The application to be developed must accept as input a file with the
description of the graph to be considered. Such description must obey
the following pattern: the first input line has the integer N
representing the number of nodes in the graph, followed by N lines
each representing the links between pairs of nodes of the graph
(similarly to the matrices shown above). For instance, the input file
describing the graph in our example looks as follows:
6
0 2 0 5 0 0
0 0 0 0 0 0
0 2 0 0 0 5
0 0 0 0 1 0
3 9 3 0 0 0
0 0 0 0 1 0
If the dimension of the matrix and the number of available processes
are not compatible with the conditions of the Fox algorithm, you must
provide an appropriate error message and the execution must be
canceled.
As output, your application must print the Df matrix representing the
solution for the problem, one row per line. For the given example, the
output should be:
0 2 9 5 6 14
0 0 0 0 0 0
9 2 0 14 6 5
4 6 4 0 1 9
3 5 3 8 0 8
4 6 4 9 1 0
The input file must be read from the standard input and the results
are to be printed to the standard output
(click here to get
a set of test examples).
What to Deliver?
A ZIP file including:
- All source code files (can be just one) implementing your solution
- A makefile that generates the executable program (assign name fox)
- Short technical report (no more than 5 pages) in PDF format
describing the work done (free structure) and including:
- A summary on the algorithm implementation (include details
about the base idea of the algorithm, main data structures,
relevant auxiliary functions, type of communications, ...)
- Performance evaluation including execution times (in
milliseconds and excluding I/O) and speedups (comparing with
sequential execution and with execution with 1 process) for, at
least, 1, 4, 9 and 16 processes
- Main difficulties encountered in the development of the work
(if any) and comments/suggestions about the work (optional)
The code must compile and execute in the machines made available in
Lab1 and that constitute your cluster. Legibility and code structure
will be valued for the final mark.
Deadline
The ZIP file (containing the items described above) must be sent
to
miguel-areias@dcc.fc.up.pt until 8th of November and
presented orally in the week after (15th of November, time to
be specified).
Cluster Setup
To avoid having to authenticate at each node every time you run MPI,
do the following:
- Generate an authentication key with the command
ssh-keygen -t rsa
This will produce two files in your home directory:
~/.ssh/id_rsa with your private key, and
~/.ssh/id_rsa.pub with your public key
- Copy your public key to the authorization_keys file with
the command:
cp ~/.ssh/id_rsa.pub ~/.ssh/authorized_keys
- Try it! The command
ssh node_xpto
should now log you in at node_xpto without needing to
type in the password



