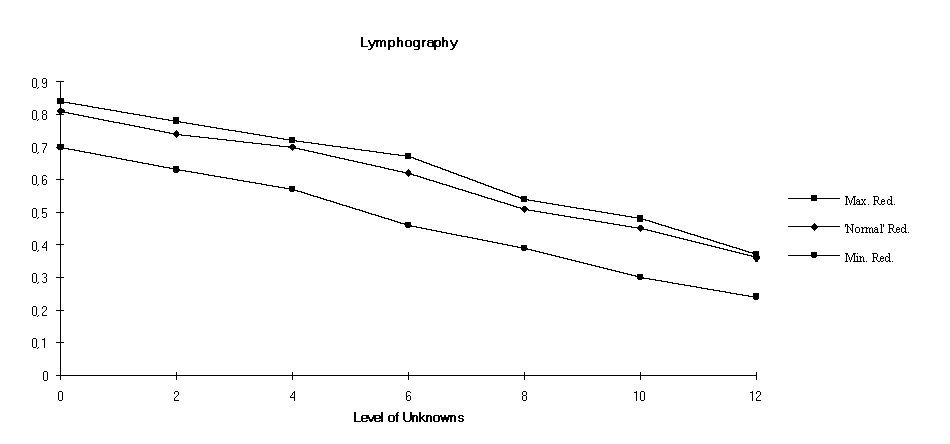
The controlled use of redundancy is one of the novel features we have explored. Although redundancy affects positively accuracy it has a negative effect on comprehensibility. This section presents a set of experiments carried out in order to observe these effects of redundancy.
The experiments consisted on varying the level of "unknown" values in the examples given for classification. For instance a level of unknowns equal to 2 means that all the examples used in classification had 2 of their attributes with their values changed into "unknown". The choice of the 2 attributes was made at random for each example. Having the examples changed in that way three classification strategies (with different levels of redundancy) were tried and the results observed. The results presented below are all averages of 10 runs.
The three different classification strategies tested are labelled in the graphs below as "Redund.+", "Redund." and "Redund.-", respectively. The first consists on using all the learned rules thus not making any splitting between the foreground and the background set of rules (c.f. section 3.1). The second is the normal classification strategy of YAILS, with some level of static redundancy and dynamic redundancy. The last corresponds to a minimal amount of static redundancy and no dynamic redundancy. The accuracy results are given in figure 2.

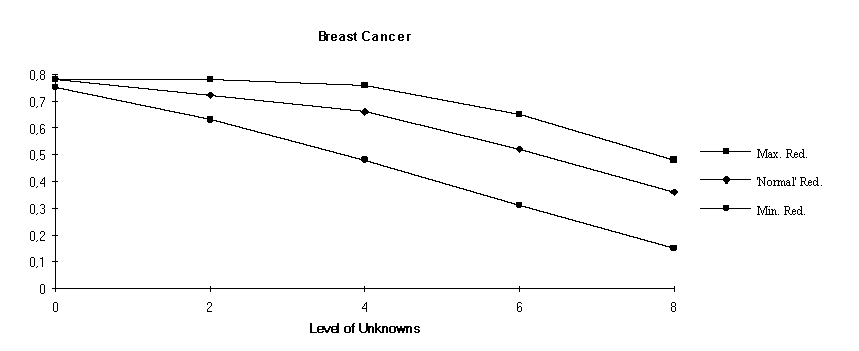
Redundancy has a negative effect on simplicity. The decision of what tradeoff should be between accuracy and comprehensibility is made by the user. The cost can be high in terms of number of rules. For instance in the Lymphography experiment the "Redund.+" strategy used a theory consisting of 28, rules while the "Redund.-" used only 6 rules. The "Redund." strategy is in between, but as the level of unknowns grows, it approaches the level of "Redund.+" thanks to dynamic redundancy. The gap is not so wide in the Breast Cancer experiment but still, there is a significant difference.
In summary, these experiments show the advantage of redundancy in terms of accuracy. This gain is sometimes related to the amount of "unknown" values present in the examples, but not always. Redundancy can be a good method to fight the problem of "unknowns", but the success depends also on other characteristics of the dataset.