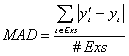
The goal of the evaluation function is to compare two rules (one being a specialization of the other). There are two consequences of specializing a rule. We have a gain in terms of fitting, but we loose coverage as the domain is restricted[4]. The evaluation function should weigh these factors producing a quality measure of the specialization that enables the comparison to the original rule. R2 uses a weighted average of these two factors as evaluation function.
R2 measures the degree of fitting of a model using a statistic called Mean Absolute Deviation (MAD) which is defined in equation 1 :
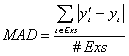
| (1)
|
Coverage is measured by the number of examples that satisfy the rule. Notice that we start this specialization process with a rule and we are trying to compare it with its specializations. For each candidate specialization we calculate the gain in fitting error and the loss in coverage compared to this original rule. These factors are calculated by :
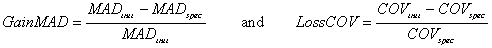
| (2)
|
The quality of the candidate specialization is calculated as a weighted average of these two values[5]. It remains an open question how to set the weight of each of the factors. These weights represent a trade-off between generality and correctness of the learned rules. The bigger the weight on GainMAD the more specific the rules get. As a result the final theory will probably have too many rules. On the contrary, if we favor coverage we will get fewer rules but probably less accurate. This can be interesting in noisy domains where we don't want to overfit the noise by producing too specific rules. As this is highly domain dependent we let the user tune these weights[6]. R2 introduces a further degree of flexibility by allowing some limited variation on these weights, as we will explain below. The formula for calculating the quality of a specialization is as follows :
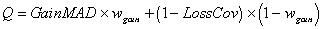
| (3)
|
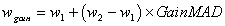
| (4)
|
We will now illustrate these ideas with the example we have been using. Imagine that after the step of building a model for an uncovered region we have as result the rule R3 previously shown. Suppose that this rule covers 15 examples and has a MAD of 0.45. One possible specialization of this rule could be :
R31 IF X3 5 X2 < 2 THEN Y = -4.2 + 0.6 X4 + 0.99 X2
Notice that this rule has as conclusion a refined model of the one in the original rule R3. This is a consequence of the change of the set of examples that the rule is covering. If this new rule covered only 12 of the previous examples but had a MAD of 0.24 then we would get :
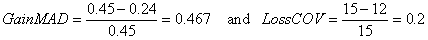
If the interval for the weight on GainMAD was [0.6..0.85] then wgain would be given by 0.6 + (0.85-0.6) 0.467 = 0.717, and finally the quality of this specialization would be:
Q = 0.467 0.717 + (1-0.2) (1-0.717) =0.561
R2 would now compare this value to the quality of the original rule and decide whether this specialization is better.
We still did not refer how the quality of the original rule is assessed[7]. We decided to use the difference 1-MAD has the quality of these original models[8]. In this case rule R3 would have a value of 0.55. This makes the specialization more attractive and the next step followed by R2 would be to try to specialize this new rule and so on until no better specialization of the current best rule exists.