3.1 Using Certainty Factors (MYCIN)

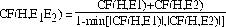
MYCIN [11] is one of the best known expert systems. MYCIN uses certainty factors (CF) as a way of modelling reasoning under uncertainty. A certainty factor is a number between -1 and 1 that represents the change in our belief on some hypothesis. A positive number means an increase in the belief and a negative number the contrary. A value of 0 means that there is no change in our belief on the hypothesis. In this work we are particularly interested in the parallel combination of rules, i.e. given E1 _ H and E2 _ H together with their respective confidence factors we are interested on the confidence factor of H given that E1 and E2 are true. The formulas used for rule combination in MYCIN are the following :

If CF(H,E1) and CF(H,E2) have opposite signs :

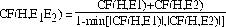
(1)

If CF(H,E1) and CF(H,E2) are both greater or equal to zero :

CF(H,E1E2) = CF(H,E1)+CF(H,E2)-CF(H,E1)CF(H,E2)

(2)

If CF(H,E1) and CF(H,E2) are both less than zero :

CF(H,E1E2) = CF(H,E1)+CF(H,E2)+CF(H,E1)CF(H,E2)

(3)

For the probabilistic definition of CF's we use the following [7] :

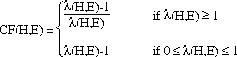
(4)

where

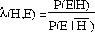
This formalisation is derived from a set of axioms [7] which imply that the rules must be conditionally independent given the hypothesis and its negation [9]. This assumption does not hold in general. Nevertheless, this approach has been widely used and achieved good practical results.