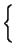
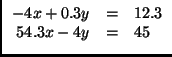
Por vezes poderemos estar interessados em armazenar a nossa informação em estruturas de dados com mais do que uma dimensão, como é o caso dos vectores. As matrizes arranjam a informação em duas dimensões. Em R, as matrizes não são mais do que vectores com uma propriedade especial que é a dimensão. Vejamos um exemplo. Suponhamos que temos doze números correspondentes às vendas trimestrais durante o último ano, em três lojas. As instruções seguintes permitem ``organizar'' esses números como uma matriz,
> vendas <- c(45,23,66,77,33,44,56,12,78,23,78,90)
> vendas
[1] 45 23 66 77 33 44 56 12 78 23 78 90
> dim(vendas) <- c(3,4)
> vendas
[,1] [,2] [,3] [,4]
[1,] 45 77 56 23
[2,] 23 33 12 78
[3,] 66 44 78 90
Repare como os números foram ``espalhados'' por uma matriz com 3 linhas e 4 colunas, que foi a dimensão que atribuímos ao vector vendas através da função dim(). Na realidade seria mais simples criar a matriz usando uma função específica para isso,
> vendas <- matrix(c(45,23,66,77,33,44,56,12,78,23,78,90),3,4)
Como eventualmente terá reparado os números foram ``espalhados'' pela matriz por coluna, i.e. primeiro foi preenchida a primeira coluna, depois a segunda, etc. Caso não seja isto o que pretendemos, poderemos preencher a matriz por linhas da seguinte forma,
> vendas <- matrix(c(45,23,66,77,33,44,56,12,78,23,78,90),3,4,byrow=T)
> vendas
[,1] [,2] [,3] [,4]
[1,] 45 23 66 77
[2,] 33 44 56 12
[3,] 78 23 78 90
Nas matrizes também é possível dar nomes aos elementos para tornar a leitura da informação mais legível. Vejamos como fazer isso para a nossa matriz de vendas trimestrais nas 3 lojas,
> rownames(vendas) <- c('loja1','loja2','loja3')
> colnames(vendas) <- c('1.trim','2.trim','3.trim','4.trim')
> vendas
1.trim 2.trim 3.trim 4.trim
loja1 45 23 66 77
loja2 33 44 56 12
loja3 78 23 78 90
Como a visualização das matrizes sugere, podemos aceder aos elementos individuais das matrizes usando um esquema de indexação semelhante ao dos vectores, mas desta vez com dois índices (as dimensões da matriz),
> vendas[2,2] [1] 44
Ou então, tirando partido dos nomes,
> vendas['loja2','2.trim'] [1] 44
De igual modo, podemos tirar partido dos esquemas de indexação discutidos na Secção 1.8 para seleccionar elementos das matrizes, como mostram os seguintes exemplos,
> vendas[-2,2]
loja1 loja3
23 23
> vendas[1,-c(2,4)]
1.trim 3.trim
45 66
Podemos mesmo omitir uma das dimensões das matrizes para deste modo obter todos os elementos da mesma (um índice vazio),
> vendas[1,]
1.trim 2.trim 3.trim 4.trim
45 23 66 77
> vendas[,'4.trim']
loja1 loja2 loja3
77 12 90
As funções cbind() e rbind() podem ser usadas para juntar dois ou mais vectores ou matrizes, por colunas ou por linhas, respectivamente. Os seguintes exemplos ilustram o seu uso,
> m1 <- matrix(c(45,23,66,77,33,44,56,12,78,23),2,5)
> m1
[,1] [,2] [,3] [,4] [,5]
[1,] 45 66 33 56 78
[2,] 23 77 44 12 23
> cbind(c(4,76),m1[,4])
[,1] [,2]
[1,] 4 56
[2,] 76 12
> m2 <- matrix(rep(10,50),10,5)
> m2
[,1] [,2] [,3] [,4] [,5]
[1,] 10 10 10 10 10
[2,] 10 10 10 10 10
[3,] 10 10 10 10 10
[4,] 10 10 10 10 10
[5,] 10 10 10 10 10
[6,] 10 10 10 10 10
[7,] 10 10 10 10 10
[8,] 10 10 10 10 10
[9,] 10 10 10 10 10
[10,] 10 10 10 10 10
> m3 <- rbind(m1[1,],m2[5,])
> m3
[,1] [,2] [,3] [,4] [,5]
[1,] 45 66 33 56 78
[2,] 10 10 10 10 10
As regras aritméticas e de reciclagem que estudamos anteriormente, também se aplicam às matrizes. Vejamos uns pequenos exemplos,
> m <- matrix(c(45,23,66,77,33,44,56,12,78,23),2,5)
> m
[,1] [,2] [,3] [,4] [,5]
[1,] 45 66 33 56 78
[2,] 23 77 44 12 23
> m*3
[,1] [,2] [,3] [,4] [,5]
[1,] 135 198 99 168 234
[2,] 69 231 132 36 69
> m1 <- matrix(c(45,23,66,77,33,44),2,3)
> m1
[,1] [,2] [,3]
[1,] 45 66 33
[2,] 23 77 44
> m2 <- matrix(c(12,65,32,7,4,78),2,3)
> m2
[,1] [,2] [,3]
[1,] 12 32 4
[2,] 65 7 78
> m1+m2
[,1] [,2] [,3]
[1,] 57 98 37
[2,] 88 84 122
A aplicação das operações a matrizes (como no exemplo ``> m*3'' apresentado acima), funciona elemento a elemento como no caso dos vectores. Isto significa que se um operando é menor ele é reciclado até perfazer o tamanho do maior. No entanto, o R também possui operadores especiais para as usuais operações da álgebra matricial. Por exemplo a multiplicação de duas matrizes pode ser feita da seguinte forma,
> m1 <- matrix(c(45,23,66,77,33,44),2,3)
> m1
[,1] [,2] [,3]
[1,] 45 66 33
[2,] 23 77 44
> m2 <- matrix(c(5,3,466,54.5,3.2,-34),3,2)
> m2
[,1] [,2]
[1,] 5 54.5
[2,] 3 3.2
[3,] 466 -34.0
> m1 %*% m2
[,1] [,2]
[1,] 15801 1541.7
[2,] 20850 3.9
Atente no operador especial (%*%) para simbolizar que se trata da multiplicação matricial e não a usual multiplicação. A multiplicação matricial tem, como é sabido, regras especiais no que concerne, por exemplo, à dimensão das matrizes envolvidas, pelo que não poderá ser usada com quaisquer matrizes.
Ainda no contexto da álgebra matricial, o R tem muitas outras funções, como por exemplo a função t para obter a transposta de uma matriz quadrada,
> t(m1)
[,1] [,2]
[1,] 45 23
[2,] 66 77
[3,] 33 44
ou a função det para calcular o determinante de uma matriz,
> m <- matrix(c(34,-23,43,5),2,2) > det(m) [1] 1159
É também possível usar a função solve para obter a inversa de uma matriz,
> solve(m)
[,1] [,2]
[1,] 0.004314064 -0.03710095
[2,] 0.019844694 0.02933563
Finalmente, esta mesma função pode ser usada para resolver sistemas de equações. Imaginemos o seguinte sistema de equações,
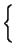
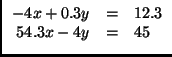
Podemos resolvê-lo em R da seguinte forma,
> coefs <- matrix(c(-4,0.3,54.3,-4),2,2,byrow=T) > ys <- c(12.3,45) > solve(coefs,ys) [1] 216.2069 2923.7586