The existence of unknown values on the examples originates problems in two "places" during the learning process of YAILS. One of them is when YAILS tries to known if an example, which has unknown values, satisfies some rule. The other case is when YAILS tries to find which examples a rule covers. In effect these two problems are inverse one of another because if an example satisfies a rule this means that it belongs to the set of examples covered by the rule. This fact is reflected in the way YAILS treats both cases.
An example satisfies a rule if it satisfies all its conditions. In the case were the example has an unknown value on some condition of the rule, YAILS calculates a conditional probability of the value of the example being exactly the one stated on the rule. If this probability is higher than some threshold (which is one of the user-definable parameters) then YAILS assumes that the examples satisfies the rule. Stating it in a formal way :
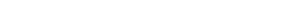
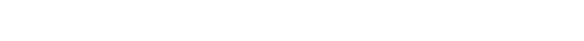
where
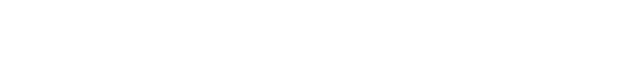
Inorder to better illustrate the concept of satisfaction observe the following example :
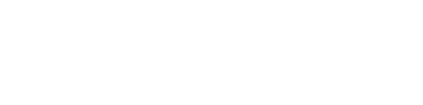
As said before the problem of knowing which examples a rule covers is inverse of this one so YAILS uses the same probabilistic approximation to solve it.