

Evaluation Methodologies
Fraud Detection Course - 2020/2021
Nuno Moniz
nuno.moniz@fc.up.pt
Today
- Evaluation Methodologies
Evaluation Methodologies
Performance Estimation
The setting
- Predictive task: unknown function \(Y = f(x)\) that maps the values of a set of predictors into a target variable value (can be a classification or a regression problem)
- A (training) data set \({< \mathbf{x_i},y_i >}_{i=1}^N\), with known values of this mapping
- Performance evaluation criterion(a) - metric(s) of predictive performance (e.g. error rate or mean squared error)
- How to obtain a reliable estimates of the predictive performance of any solutions we consider to solve the task using the available data set?
Reliability of Estimates
Resubstitution estimates
- Given that we have a data set one possible way to obtain an estimate of the performance of a model is to evaluate it on this data set
- This leads to what is known as a resubstitution estimate of the prediction error
- These estimates are unreliable and should not be used as they tend to be over-optimistic!
Reliability of Estimates
Resubstitution estimates (2)
- Why are they unreliable?
- Models are obtained with the goal of optimizing the selected prediction error statistic on the given data set
- In this context it is expected that they get good scores!
- The given data set is just a sample of the unknown distribution of the problem being tackled
- What we would like is to have the performance of the model on this distribution
- As this is usually impossible the best we can do is to evaluate the model on new samples of this distribution
Goal of Performance Estimation
Main Goal of Performance Estimation Obtain a reliable estimate of the expected prediction error of a model on the unknown data distribution
- In order to be reliable it should be based on evaluation on unseen cases - a test set
Goal of Performance Estimation (2)
- Ideally we want to repeat the testing several times
- This way we can collect a series of scores and provide as our estimate the average of these scores, together with the standard error of this estimate
- In summary:
- calculate the sample mean prediction error on the repetitions as an estimate of the true population mean prediction error
- complement this sample mean with the standard error of this estimate
Goal of Performance Estimation (3)
The golden rule of Performance Estimation: The data used for evaluating (or comparing) any models cannot be seen during model development.
Goal of Performance Estimation (4)
- An experimental methodology should:
- Allow obtaining several prediction error scores of a model, \(E_1, E_2, \cdots, E_k\)
- Such that we can calculate a sample mean prediction error \(\bar{E} = \frac{1}{K} \sum_{i=1}^k E_i\)
- And also the respective standard error of this estimate \(SE(\bar{E}) = \frac{S_E}{\sqrt{k}}\)
- where \(S_E\) is the sample standard deviation of \(E\) measured as \(\sqrt{\frac{1}{k-1} \sum_{i=1}^k (E_i - \bar{E})^2}\)
The Holdout Method and Random Subsampling
- The holdout method consists on randomly dividing the available data sample in two sub-sets - one used for training the model; and the other for testing/evaluating it
- A frequently used proportion is 70% for training and 30% for testing
The Holdout Method (2)
- If we have a small data sample there is the danger of either having a too small test set (unreliable estimates as a consequence), or removing too much data from the training set (worse model than what could be obtained with the available data)
- We only get one prediction error score - no average score nor standard error
- If we have a very large data sample this is actually the preferred evaluation method
Random Subsampling
- The Random Subsampling method is a variation of holdout method and it simply consists of repeating the holdout process several times by randomly selecting the train and test partitions
- Has the same problems as the holdout with the exception that we already get several scores and thus can calculate means and standard errors
- If the available data sample is too large the repetitions may be too demanding in computation terms
The Holdout method in R
library(DMwR)
data(Boston, package='MASS')
## random selection of the holdout
trPerc <- 0.7
sp <- sample(1:nrow(Boston), as.integer(trPerc * nrow(Boston)))
## division in two samples
tr <- Boston[sp,]
ts <- Boston[-sp,]
## obtaining the model and respective predictions on the test set
m <- rpartXse(medv ~ ., tr)
p <- predict(m, ts)
## evaluation
regr.eval(ts$medv, p, train.y = tr$medv)
## mae mse rmse mape nmse nmae
## 3.0525037 17.9729392 4.2394503 0.1619334 0.2558434 0.5084804
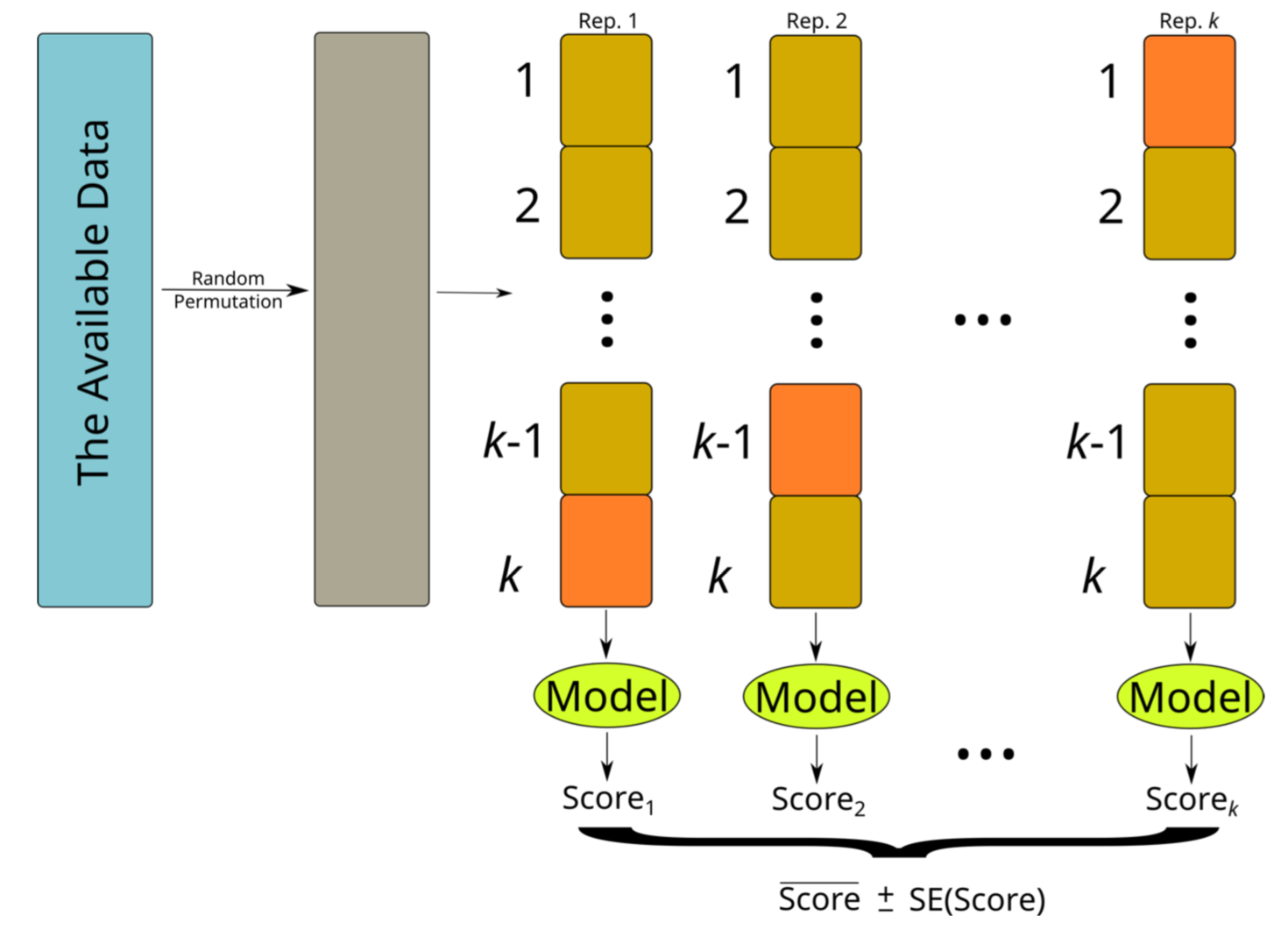
The k-fold Cross Validation Method
- The idea of k-fold Cross Validation (CV) is similar to random subsampling
- It essentially consists of k repetitions of training on part of the data and then test on the remaining
- The diference lies on the way the partitions are obtained
The k-fold Cross Validation Method (cont.)
Leave One Out Cross Validation Method (LOOCV)
- Similar idea to k-fold Cross Validation (CV) but in this case on each iteration a single case is left out of the training set
- This means it is essentially equivalent to n-fold CV, where n is the size of the available data set
The Bootstrap Method
- Train a model on a random sample of size n with replacement from the original data set (of size n)
- Sampling with replacement means that after a case is randomly drawn from the data set, it is "put back on the sampling bag"
- This means that several cases will appear more than once on the training data
- On average only 63.2% of all cases will be on the training set
- Test the model on the cases that were not used on the training set
- Repeat this process many times (typically around 200)
- The average of the scores on these repetitions is known as the bootstrap estimate
- The \(.632\) bootstrap estimate is obtained by \(.368 \times \epsilon_r + .632 \times \epsilon_0\), where \(\epsilon_r\) is the resubstitution estimate
Bootstrap in R
data(Boston, package='MASS')
nreps <- 200
scores <- vector("numeric", length = nreps)
n <- nrow(Boston)
for(i in 1:nreps) {
# random sample with replacement
sp <- sample(n, n, replace = TRUE) # data splitting
tr <- Boston[sp,]
ts <- Boston[-sp,]
# model learning and prediction
m <- lm(medv ~ ., tr)
p <- predict(m, ts)
# evaluation
scores[i] <- mean((ts$medv - p)^2)
}
# calculating means and standard errors
summary(scores)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 13.97 21.90 24.12 24.62 26.66 39.11
The Infra-Structure of package performanceEstimation
- The package performanceEstimation provides a set of functions that can be used to carry out comparative experiments of different models on different predictive tasks
- This infra-structure can be applied to any model/task/evaluation metric
- Installation:
- Official release (from CRAN repositories):
install.packages("performanceEstimation")
The Infra-Structure of package performanceEstimation
- The main function of the package is
performanceEstimation() - It has 3 arguments:
- The predictive tasks to use in the comparison
- The models to be compared
- The estimation task to be carried out
- The function implements a wide range of experimental methodologies including all we have discussed
A Simple Example
- Suppose we want to estimate the mean squared error of regression trees in a certain regression task using cross validation
library(performanceEstimation)
library(DMwR)
data(Boston,package='MASS')
res <- performanceEstimation(PredTask(medv ~ ., Boston),
Workflow("standardWF", learner="rpartXse"),
EstimationTask(metrics="mse", method=CV(nReps = 1, nFolds = 10)))
##
##
## ##### PERFORMANCE ESTIMATION USING CROSS VALIDATION #####
##
## ** PREDICTIVE TASK :: Boston.medv
##
## ++ MODEL/WORKFLOW :: rpartXse
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
A Simple Example (2)
summary(res)
## Length Class Mode
## Boston.medv 1 -none- list
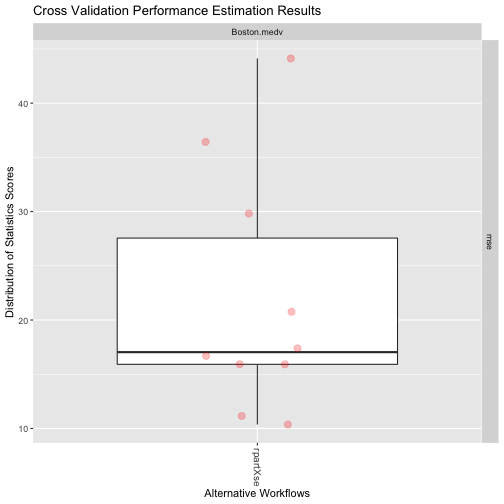
A Simple Example (3)
plot(res)
Predictive Tasks
- Objects of class PredTask describing a predictive task
- Classification
- Regression
- Time series forecasting
- Created with the constructor with the same name
data(iris)
PredTask(Species ~ ., iris)
## Prediction Task Object:
## Task Name :: iris.Species
## Task Type :: classification
## Target Feature :: Species
## Formula :: Species ~ .
## <environment: 0x7f93149f29b8>
## Task Data Source :: iris
Workflows
- Objects of class Workflow describing an approach to a predictive task
- Standard Workflows
- Function
standardWFfor classification and regression - Function
timeseriesWFfor time series forecasting
- Function
- User-defined Workflows
- Standard Workflows
Standard Workflows for Classification and Regression Tasks
library(e1071)
Workflow("standardWF", learner = "svm", learner.pars = list(cost = 10, gamma = 0.1))
## Workflow Object:
## Workflow ID :: svm
## Workflow Function :: standardWF
## Parameter values:
## learner -> svm
## learner.pars -> cost=10 gamma=0.1
Standard Workflows for Classification and Regression Tasks
"standardWF" can be omitted ...
Workflow(learner="svm", learner.pars = list(cost = 5))
## Workflow Object:
## Workflow ID :: svm
## Workflow Function :: standardWF
## Parameter values:
## learner -> svm
## learner.pars -> cost=5
Standard Workflows for Classification and Regression Tasks
- Main parameters of the constructor:
- Learning stage
learner- which function is used to obtain the model for the training datalearner.par` - list with the parameter settings to pass to the learner
- Prediction stage
predictor- function used to obtain the predictions (defaults topredict()) +`predictor.pars- list with the parameter settings to pass to the predictor
- Learning stage
Standard Workflows for Classification and Regression Tasks
- Main parameters of the constructor:
- Data pre-processing
pre- vector with function names to be applied to the training and test sets before learningpre.pars- list with the parameter settings to pass to the functions
- Predictions post-processing
post- vector with function names to be applied to the predictionspost.pars- list with the parameter settings to pass to the functions
- Data pre-processing
Standard Workflows for Classification and Regression Tasks
data(algae, package="DMwR")
res <- performanceEstimation(PredTask(a1 ~ ., algae[, 1:12], "A1"),
Workflow(learner = "lm", pre = "centralImp", post = "onlyPos"),
EstimationTask("mse", method = CV())) # defaults to 1x10-fold CV
##
##
## ##### PERFORMANCE ESTIMATION USING CROSS VALIDATION #####
##
## ** PREDICTIVE TASK :: A1
##
## ++ MODEL/WORKFLOW :: lm
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
Evaluating Variants of Workflows
Function workflowVariants()
library(e1071)
data(Boston,package="MASS")
res2 <- performanceEstimation(PredTask(medv ~ .,Boston),
workflowVariants(learner="svm",learner.pars=list(cost=1:5,gamma=c(0.1,0.01))),
EstimationTask(metrics="mse",method=CV()))
##
##
## ##### PERFORMANCE ESTIMATION USING CROSS VALIDATION #####
##
## ** PREDICTIVE TASK :: Boston.medv
##
## ++ MODEL/WORKFLOW :: svm.v1
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v2
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v3
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v4
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v5
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v6
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v7
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v8
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v9
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm.v10
## Task for estimating mse using
## 1 x 10 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
Evaluating Variants of Workflows (cont.)
summary(res2)
## Length Class Mode
## Boston.medv 10 -none- list
Exploring the Results
getWorkflow("svm.v1", res2)
## Workflow Object:
## Workflow ID :: svm.v1
## Workflow Function :: standardWF
## Parameter values:
## learner.pars -> cost=1 gamma=0.1
## learner -> svm
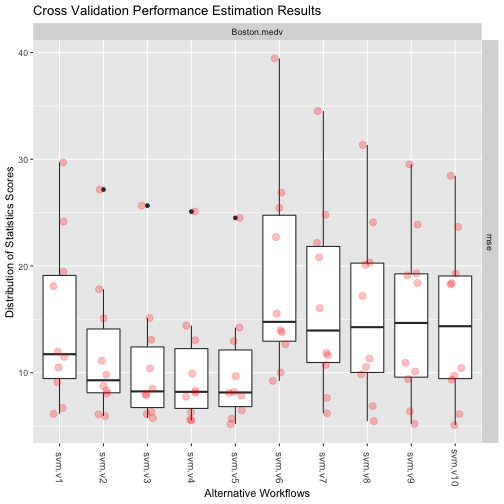
topPerformers(res2)
## $Boston.medv
## Workflow Estimate
## mse svm.v5 10.287
Visualizing the Results
plot(res2)
Estimation Tasks
- Objects of class EstimationTask describing the estimation task
- Main parameters of the constructor
- metrics - vector with names of performance metrics
- method - object of class EstimationMethod describing the method used to obtain the estimates
- Main parameters of the constructor
EstimationTask(metrics = c("F", "rec", "prec"), method = Bootstrap(nReps = 100))
## Task for estimating F,rec,prec using
## 100 repetitions of e0 Bootstrap experiment
## Run with seed = 1234
Performance Metrics
- Many classification and regression metrics are available
- Check the help page of functions
classificationMetricsandregressionMetrics
- Check the help page of functions
- User can provide a function that implements any other metric she/he wishes to use
- Parameters evaluator and evaluator.pars of the
EstimationTaskconstructor
- Parameters evaluator and evaluator.pars of the
Comparing Different Algorithms on the Same Task
library(randomForest)
library(e1071)
res3 <- performanceEstimation(PredTask(medv ~ ., Boston),
workflowVariants("standardWF",learner=c("rpartXse","svm","randomForest")),
EstimationTask(metrics="mse",method=CV(nReps=2,nFolds=5)))
##
##
## ##### PERFORMANCE ESTIMATION USING CROSS VALIDATION #####
##
## ** PREDICTIVE TASK :: Boston.medv
##
## ++ MODEL/WORKFLOW :: rpartXse
## Task for estimating mse using
## 2 x 5 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: svm
## Task for estimating mse using
## 2 x 5 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
##
##
## ++ MODEL/WORKFLOW :: randomForest
## Task for estimating mse using
## 2 x 5 - Fold Cross Validation
## Run with seed = 1234
## Iteration :**********
Some auxiliary functions
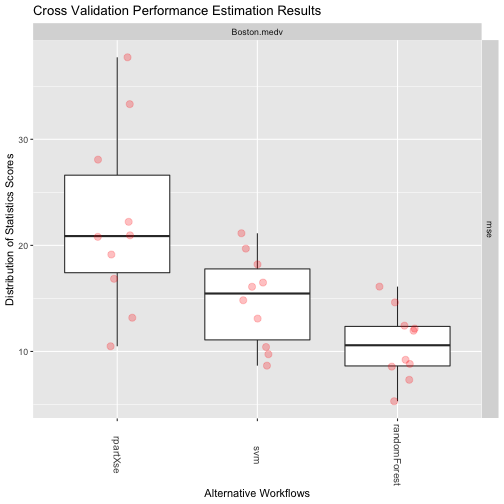
rankWorkflows(res3, 3)
## $Boston.medv
## $Boston.medv$mse
## Workflow Estimate
## 1 randomForest 10.65158
## 2 svm 14.83765
## 3 rpartXse 22.27489
The Results
plot(res3)
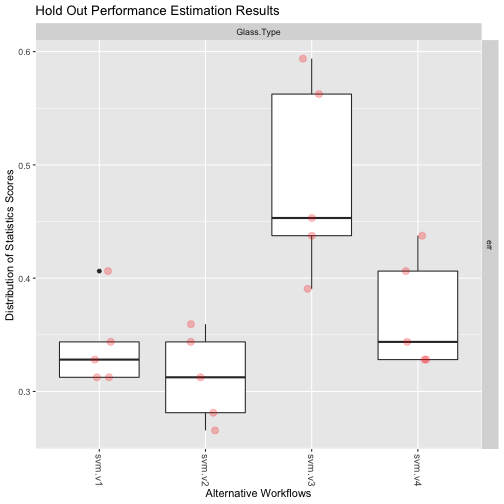
An example using Holdout and a classification task
data(Glass,package='mlbench')
res4 <- performanceEstimation(PredTask(Type ~ ., Glass),
workflowVariants(learner="svm", # You may omit "standardWF" !
learner.pars=list(cost=c(1,10),gamma=c(0.1,0.01))),
EstimationTask(metrics="err",method=Holdout(nReps=5,hldSz=0.3)))
##
##
## ##### PERFORMANCE ESTIMATION USING HOLD OUT #####
##
## ** PREDICTIVE TASK :: Glass.Type
##
## ++ MODEL/WORKFLOW :: svm.v1
## Task for estimating err using
## 5 x 70 % / 30 % Holdout
## Run with seed = 1234
## Iteration : 1 2 3 4 5
##
##
## ++ MODEL/WORKFLOW :: svm.v2
## Task for estimating err using
## 5 x 70 % / 30 % Holdout
## Run with seed = 1234
## Iteration : 1 2 3 4 5
##
##
## ++ MODEL/WORKFLOW :: svm.v3
## Task for estimating err using
## 5 x 70 % / 30 % Holdout
## Run with seed = 1234
## Iteration : 1 2 3 4 5
##
##
## ++ MODEL/WORKFLOW :: svm.v4
## Task for estimating err using
## 5 x 70 % / 30 % Holdout
## Run with seed = 1234
## Iteration : 1 2 3 4 5
The Results
plot(res4)
Hands on Performance Estimation
Load in the data set algae and answer the following questions:
Estimate the MSE of a regression tree for forecasting alga a1 using 10-fold Cross validation.
Repeat the previous exercise this time trying some variants of random forests. Check what are the characteristics of the best performing variant.
Compare the results in terms of mean absolute error of the default variants of a regression tree, a linear regression model and a random forest, in the task of predicting alga a3. Use 2 repetitions of a 5-fold Cross Validation experiment.
Carry out an experiment designed to select what are the best models for each of the seven harmful algae. Use 10-fold Cross Validation. For illustrative purposes consider only the default variants of regression trees, linear regression and random forests.
