Pesquisa

Problema de pesquisa

Suponhamos que temos uma sequência de \(n\) valores (e.g. inteiros) \[ v[0], v[1], v[2], \ldots, v[n-1] \]

Queremos saber se um valor \(x\) ocorre na sequência, isto é:

Pesquisa sequencial

Já vimos um algoritmo para resolver este problema, a pesquisa sequencial:

1. Para \(i\) de \(0\) até \(n-1\):
   • se \(v[i] = x\) então terminamos com resposta \(i\);
   • caso contrário, continuamos a pesquisa
2. Se chegamos ao fim do ciclo, então \(x\) não ocorre na sequência

Pesquisa sequencial em C

int pesquisa_seq(int vec[], int n, int x)
{
   for(int i = 0; i < n; i++) {
      if(vec[i] == x)
         return i; // encontrou 
   }
   return -1;      // não encontrou
}

Observações

• Duas formas de terminar o ciclo:
  1. se encontramos i tal que vec[i] == x
  2. ou se esgotarmos todos os índices válidos
     (e nesse caso i == n)
• No pior caso temos de percorrer todos os valores da sequência
  • quando o valor não ocorre na sequência

Alternativa

• Colocamos o valor a procurar val na posição após o último valor vec[n]
  • usada como sentinela para terminar a pesquisa
  • utiliza uma posição extra no vetor
• Permite juntar as duas condições de terminação numa só:
  • terminamos quando vec[i] == x
• Um pouco mais eficiente
  • evitamos o teste i < n na condição do ciclo

Pesquisa sequencial com sentinela

int pesquisa_seq(int vec[], int n, int x)
{
   int i, t;   // t é "temporário"
   t = vec[n]; // guardar o estado inicial
   vec[n] = x; // colocar a "sentinela" 

   i = 0;
   while(vec[i] != x)   // procurar
     i++;

   vec[n] = t;  // repor estado inicial
   // testar se encontrou e retornar
   if(i < n) return i; else return -1;
}

Pesquisa sequencial: análise

• No pior caso, o ciclo executa \(n\) vezes
  • \(n\) é o comprimento da sequência
• O tempo aumenta de forma linear com \(n\):
  • para \(n\) valores demora \(\approx T\)
  • para \(2n\) valores demora \(\approx 2T\)
  • para \(3n\) valores demora \(\approx 3T\)
  • ...

Pesquisa binária

• Queremos procurar \(x\) numa sequência de \(n\) valores inteiros \[ v[0], v[1], v[2], \ldots, v[n-1] \]
• Pré-condição: os valores estão por ordem crescente:
  • cada valor é menor ou igual ao seguinte

\[ v[0] \leq v[1] \leq v[2] \leq \cdots \leq v[n-2] \leq v[n-1] \]

Pesquisa binária: ideia

• Consideramos o índice do meio \(k = \lfloor(n-1)/2\rfloor\)
• Se \(x = v[k]\) então encontramos o valor
• Se \(x < v[k]\) então continuamos a procurar na sub-sequência \[v[0], \ldots, v[k-1]\]
• Se \(x > v[k]\) então continuamos a procurar na sub-sequência \[v[k+1], \ldots, v[n-1]\]
• Repetimos até encontrar o valor ou a sequência ficar vazia

Pesquisa binária: algoritmo

Dois índices sobre a variável indexada:

• \(i\) é o limite inferior da sub-sequência
• \(j\) é o limite superior da sub-sequência

Se o valor \(x\) ocorre na sequência original então tem de estar entre \(i\) e \(j\).

Pesquisa binária: algoritmo

\[ \begin{array}{l} i \leftarrow 0\\ j \leftarrow n-1\\ \text{Repetir enquanto}~ i \leq j:\\ \qquad k\leftarrow i + \lfloor (j-i)/2\rfloor \\ \qquad \text{se}~ x=v[k]~ \text{então terminamos com resposta}~ k \\ \qquad \text{se}~ x<v[k]~ \text{então}~ j \leftarrow k-1 \\ \qquad \text{se}~ x>v[k]~ \text{então}~ i \leftarrow k+1 \\ \text{No chegamos ao final do ciclo: o valor não ocorre} \end{array} \]

Pesquisa binária em C

int pesquisa_bin(int vec[], int n, int x) {
  int i = 0, j = n-1;

  while (i <= j)  {
    int k = i + (j-i)/2; // ponto médio
    if(vec[k] == x)
      return k;   // encontrou
    else if (x > vec[k]) 
      i = k+1;  //  x > vec[k]
    else    
      j = k-1;  //  x < vec[k]
  }
  // no final do ciclo: i > j 
  return -1; 
}

Quantas vezes executa o ciclo?

• Cada iteração divide a sequência aproximadamente a meio
• O tamanho inicial é \(n\); logo, após \(i\) iterações será \[ n\times \underbrace{\frac{1}{2} \times \frac{1}{2}\times \cdots\times \frac{1}{2}}_{i~\text{vezes}} = \frac{n}{2^i} \]
• O ciclo têm de terminar se o tamanho for inferior a 1: \[ \frac{n}{2^i} < 1 \iff i > \log_2 n \] ou seja: no pior caso fazemos \(\approx\log_2 n\) iterações.

Crescimento logarítmico

Exemplo para \(1000\) valores:

• a pesquisa sequencial efetua 1000 iterações
• a pesquisa binária efetua 10 iterações

Ordenação

Ordenação

• Para utilizar a pesquisa binária assumimos que a sequência está ordenada
• Vamos agora estudar algoritmos para ordenar uma sequência arbitária
• Objetivo: re-organizar os valores de forma a que fiquem por ordem ascendente ou descendente

Ordem ascendente e descendente

Seja \(v[0], v[1], \ldots, v[n-1]\) uma sequência de \(n\) valores.

A sequência está por ordem ascendente se e só se: \[ v[i] \leq v[i+1]\,, \quad \text{para}~ 0\leq i\leq n-2 \]

A sequência está por ordem descendente se e só se: \[ v[i] \geq v[i+1]\,, \quad \text{para}~ 0\leq i\leq n-2 \]

Nas definições acima usamos \(\leq\) e \(\geq\) para permitir valores repetidos.

Algoritmos de ordenação

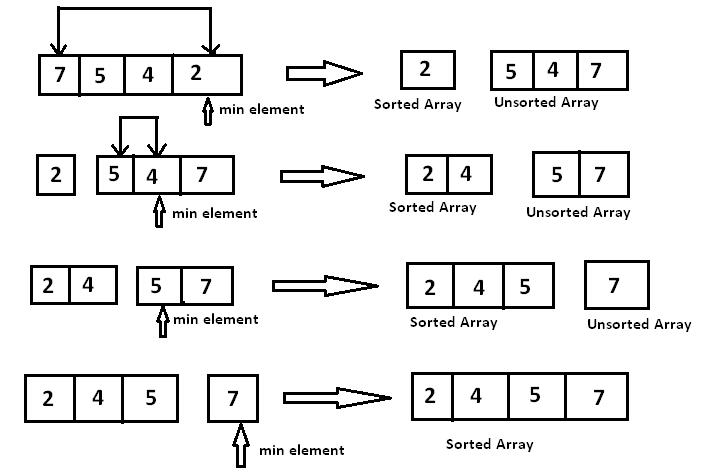
Vamos ver um algoritmo clássicos de ordenação por seleção ("selection sort").

Assumimos:

• valores inteiros
• vamos colocar por ordem crescente
• vamos modificar a variável indexada original

Ordenação por seleção

Ordenação por seleção

1. Procuramos o menor valor da sequência e trocamos o seu lugar com o 1º elemento
2. Procuramos o menor dos valores restantes e trocamos o seu lugar com o 2º elemento
3. Continuamos este processo até colocarmos todos os elementos na posição correta

Ordenação por seleção: exemplo

Ordenação por seleção: algoritmo

Repetimos para \(i\) de 0 até \(n-1\):

1. Inicializamos \(i_{min} \leftarrow i\)
2. Para \(j\) de \(i+1\) até \(n-1\):
   • se \(v[j] < v[i_{min}]\) então \(i_{min} \leftarrow j\)
3. Se \(i\neq i_{min}\) trocamos \(v[i]\) com \(v[i_{min}]\)

Ordenação por seleção em C

void select_sort(int vec[], int n) {
  int i, j;
  for(i = 0; i < n; i++) {
    int imin = i; // índice inicial do mínimo
    for(j = i+1; j < n; j++) {
      if(vec[j] < vec[imin]) imin = j;
    }
    // trocar o mínimo com vec[i]
    if(imin != i) {
      int temp = vec[i];
      vec[i] = vec[imin];
      vec[imin] = temp;
    }
  }
}

Ordenação por seleção: invariantes

\[ \overbrace{\begin{array}{|c|c|c|} \hline \texttt{v[0]} &\cdots &\texttt{v[i-1]} \\ \hline \end{array}}^{\text{por ordem crescente}} \overbrace{\begin{array}{|c|c|c|} \hline \texttt{v[i]} & \cdots & \texttt{v[n-1]} \\ \hline \end{array}}^{\text{?}} \]

Em cada iteração do ciclo exterior, os valores entre \(0\) e \(i-1\):

1. estão por ordem crescente; e
2. são os \(i\) menores valores da sequência original.