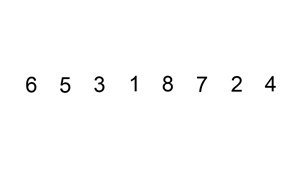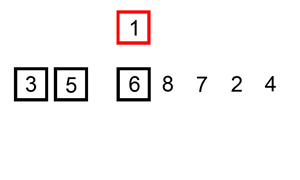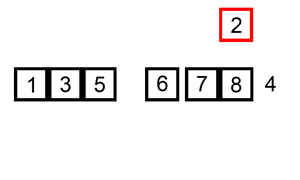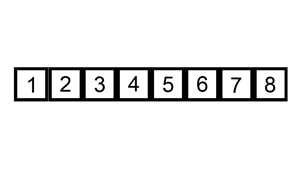Algoritmos de ordenação

Problema de ordenação

Suponhamos que temos uma sequência de \(n\) valores inteiros \[ v[0], v[1], v[2], \ldots, v[n-1] \]

Queremos colocar por ordem ascendente, isto é, trocar a ordem dos valores de forma a que no final tenhamos \[ v[0] \leq v[1] \leq v[2] \ldots \leq v[n-1] \]

Além disso, devemos preservar todos os valores originais (isto é, não podemos apagar elementos).

Algoritmos de ordenação

• Aula passada: estudamos ordenação por seleção
• Nesta aula: vamos estudar ordenação por inserção
• Vamos também comparar o custo computacional destes dois algoritmos (a sua complexidade)

Ordenação por inserção

• Vamos considerar segmentos que começam no inicio da sequência
• O segmento com apenas um valor está trivialmente ordenado
• Em cada passo vamos inserir um valor no segmento mantendo a ordem
• Analogia: a forma como um jogador que mantem uma mão de cartas ordenada
  

Ordenação por inserção: exemplo

Ordenar a sequência 6, 5, 3, 1, 8, 7, 2, 4 (animação).

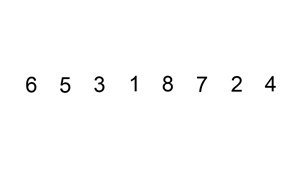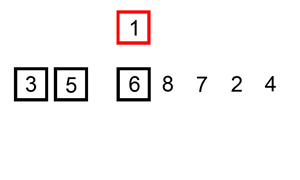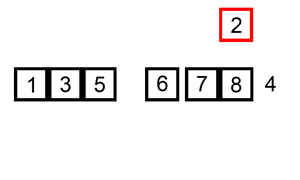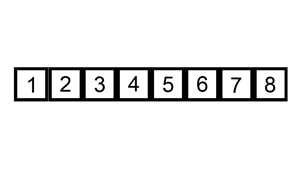
(Autor: Swfung8 via Wikimedia Commons.)

Ordenação por inserção: invariantes

\[ \overbrace{\begin{array}{|c|c|c|} \hline \texttt{v[0]} &\cdots &\texttt{v[i-1]} \\ \hline \end{array}}^{\text{por ordem crescente}} \overbrace{\begin{array}{|c|c|c|} \hline \texttt{v[i]} & \cdots & \texttt{v[n-1]} \\ \hline \end{array}}^{\text{?}} \]

Em cada iteração do ciclo exterior:

1. os valores \(v[0],\ldots,v[i-1]\) estão por ordem crescente;
2. são os mesmos valores que estavam em \(v[0], \ldots, v[i-1]\) no vetor original (eventualmente por ordem diferente)

Sub-problema: inserir em ordem

Inserir um valor \(x\) numa sequência \[ v[0] \leq v[1] \leq \ldots \leq v[i-1] \] preservando a ordem ascendente.

Ordenação por inserção: algoritmo

Basta inserir \(v[1]\), depois \(v[2]\), etc.

\[ \begin{array}{l} \text{repetir para} ~i~ \text{de}~ 1~ \text{até}~n-1:\\ \qquad x \leftarrow v[i]\\ \qquad j\leftarrow i-1 \\ \qquad \text{enquanto} ~j \geq 0 \land v[j] > x:\\ \qquad\qquad v[j+1] \leftarrow v[j]\\ \qquad \qquad j \leftarrow j -1\\ \qquad v[j+1] \leftarrow x \end{array} \]

Ordenação por inserção em C

void insert_sort(int vec[], int n) {
  int i, j;

  for(i = 1; i < n; i++) {
    int x = vec[i];
    j = i-1;
    while(j>=0 && vec[j] > x) {
      vec[j+1] = vec[j];
      j--;
    }
    vec[j+1] = x;
  }
}

Complexidade

Complexidade

• Quantas operações são necessárias para ordenar \(n\) valores?
• Este estudo chama-se análise de complexidade
• Vamos contabilizar apenas operações de comparação entre valores da sequência (<, <=, >, >=)
  • ignoramos outras operações aritméticas, acesso a memória, etc.
  • representam um custo extra fixo por cada comparação

Complexidade (cont.)

• Diferentes algoritmos podem ter complexidades diferentes
• Um algoritmo pode ter complexidade diferente dependendo dos valores de inputs
• Podemos considerar:
  • o melhor caso (pouco representativo)
  • o pior caso (péssimista)
  • o caso "médio" (mais difícil de definir)

Ordenação por seleção

Para ordenar uma sequência de \(n\) valores fazemos:

• escolher o menor de todos os valores
  (\(n-1\) comparações)
• escolher o menor dos restantes \(n-1\) valores
  (\(n-2\) comparações)
• ...
• escolher o menor de dois valores (1 comparação).

Ordenação por seleção (cont.)

O número total de comparações será então \[ n-1 + n-2 + \cdots + 1 = \frac{(n-1)n}{2} \approx n^2 \] (recordar a soma de progressões aritméticas).

Logo:

• este algoritmo tem complexidade quadrática
• a complexidade é independente dos valores da sequência

Ordenação por inserção

Melhor caso: a sequência já está ordenada.

• O ciclo exterior executa \(n-1\) vezes
• O ciclo interior while termina imediatamente

    x = vec[i]
    j = i-1;
    while(j>=0 && vec[j] > x) ...
      // vec[j] > x é FALSO

Neste caso o algoritmo efetua \(n-1\) comparações.

Ordenação por inserção

Se a sequência está ordenada ao contrário (por ordem decrescente).

• O ciclo exterior executa \(n-1\) vezes
• Os ciclos interiores executam \(1, 2, \ldots, n-1\) comparações

Logo:

• o total de comparações é \[ n-1+n-2+\cdots + 1 \approx n^2 \]
• este algoritmo tem também complexidade quadrática no pior caso

Resultados experimentais

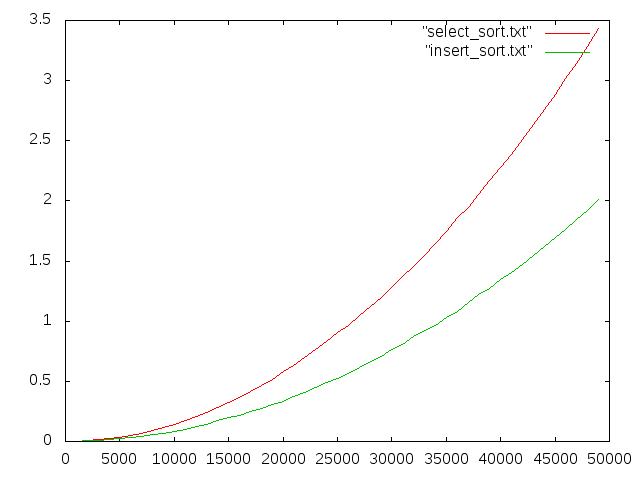
Observações

• Valores inteiros pseudo-aleatórios
• Tempos de ordenação em segundos
• A ordenação por inserção é (quase) \(2\times\) mais rápida que seleção para 50 mil valores.