Performance of Haskell programs

Bibliography

"Real World Haskell", Bryan O'Sullivan, John Goerzen & Don Stewart. Chapter 25.

Haskell performance tutorial @ CUFP, Johan Tibell:

http://blog.johantibell.com/2010/07/high-performance-haskell-tutorial-at.html

Pros and cons of high-level languages

• Haskell is a very high-level language:
  • algebraic data types, higher-order functions, type classes, lazy evaluation
  • automatic memory management (GC)
  • parallel / concurrent execution
• We do not need to specify details implementation
• We can use equational reasoning to simplify programs ("executable mathematics")
• But what about the computational process itself?
  • time spent, memory used

Reasoning about performance

• How can we measure the time and memory used?
• Given two equivalent programs, how do we choose the more efficent one?
• Given an inefficient program, how do we make it better?

Profiling

Profiling

• Compiling and executing the program in a special way to measure execution costs (space and time)
• Assign costs to centers (e.g. functions)
• Allows the programmer to identify performance bottlenecks
  • functions that consume most time
  • functions that retain most memory
  • graph memory allocation vs time by function or data type
• Objective:
  • focus optimization efforts
  • Pareto's principle: 80% of the time is spent in 20% of the code

Example: computing averages

avg :: [Double] -> Double
avg xs = sum / fromIntegral (length xs)
 -- sum :: [Double] -> Double
 -- length :: [Double] -> Int

main = do
   n <- read <$> getLine
   print (avg [1..n])

How much memory does this program use for input \(n\)?

Step 1: Collecting runtime statistics

$ stack build
$ stack exec example -- +RTS -s -RTS

• The argument -- marks the end of stack options
• Arguments between +RTS and -RTS are options for the GHC runtime system (can ommit the closing -RTS)
• RTS option -s prints a summary of runtime statistics
• No need to compile with profiling turned on

Sample output

$ echo 1e7 | stack exec example -- +RTS -s +RTS
   1,680,163,544 bytes allocated in the heap
   1,202,239,544 bytes copied during GC
     335,815,968 bytes maximum residency (13 sample(s))
      68,227,472 bytes maximum slop
             762 MB total memory in use (0 MB lost due to fragmentation)

                                     Tot time (elapsed)  Avg pause  Max pause
  Gen  0      3198 colls,     0 par    0.280s   0.303s     0.0001s    0.0003s
  Gen  1        13 colls,     0 par    0.608s   0.773s     0.0595s    0.3081s

  INIT    time    0.000s  (  0.000s elapsed)
  MUT     time    0.548s  (  0.533s elapsed)
  GC      time    0.888s  (  1.076s elapsed)
  EXIT    time    0.008s  (  0.030s elapsed)
  Total   time    1.552s  (  1.639s elapsed)

  %GC     time      57.2%  (65.7% elapsed)

  Alloc rate    3,065,991,868 bytes per MUT second

  Productivity  42.8% of total user, 34.3% of total elapsed

Overview of statistics collected

• Allocations, GC and memory usage (residency)
• Percentage of time spent on GC vs. actual computation
• For running our example (average of 10 million floats)

762 MB total memory in use
%GC     time      57.2%  (65.7% elapsed)

Why did this program use so much memory?

Step 2: Profiling

• Compile with profiling enable
• Running with profiling option for heap allocations

$ stack build --executable-profiling
$ echo 1e7 | stack exec example -- +RTS -p -hc
# generates `example.prof':

        Fri Apr 27 11:38 2018 Time and Allocation Profiling Report  (Final)

           example +RTS -p -hc -RTS

        total time  =        1.17 secs   (1171 ticks @ 1000 us, 1 processor)
        total alloc = 1,680,126,272 bytes  (excludes profiling overheads)

COST CENTRE MODULE SRC                         %time %alloc

main        Main   src/Main.hs:(10,1)-(12,20)   88.1  100.0
avg         Main   src/Main.hs:7:1-42           11.9    0.0
...

Profiling (again)

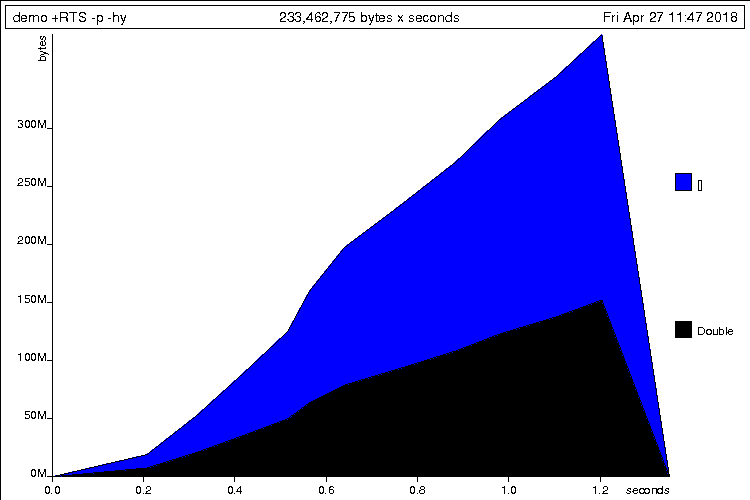
Profiling again to this time to collect heap allocation by data types.

$ stack build --executable-profiling
$ echo 1e7 | stack exec example -- +RTS -p -hy
# generates `example.prof' and `example.hp'
$ hp2ps -c -e5in example.hp
# generates `example.ps' chart

Understanding the profile

avg :: [Double] -> Double
avg xs = sum xs / fromIntegral (length xs)

main = print (avg [1..1e7])

• 88% of the time and 100% of the allocations occur in main (the list of 10 million Doubles)
• Why does avg retain the entire list rather than consume it one value at a time?
• Answer: the list cannot be deallocated while doing the sum because it is still needed for computing the length

Improving retention

avg :: [Double] -> Double
avg xs = worker xs (0,0)
  where
  worker :: [Double] -> (Double,Int) -> Double
  worker [] (s,n)     = s / fromIntegral n
  worker (x:xs) (s,n) = worker xs (x+s,1+n)

• We can compute the sum and length in one pass using a tail-recursive function
• This should allow deallocating each list node immediately as we process each number

Profiling again

Compiled with optimizations (-O2) the program uses constant space.

• 1 MB total memory in use ((independent of \(n\))
• percentage of GC time: 0.6%

Compiled without optimizations (-O0) we get worse results than before!

• 1552 MB total memory in use for \(n=\) 10 million
• percentage of GC time: 72.1%

Why this difference?

Lazy evaluation

• Haskell is a non-strict language
• Functions evaluate their arguments only if needed

cond :: Bool -> a -> a -> a
cond True x y  = x
cond False x y = y

bottom :: Int -> Int 
bottom x = bottom x

> bottom 0
 --- infinite loop, Ctrl-C
> cond True 42 (bottom 0)
42

Lazy evaluation (2)

• Non-strict semantics is implemented using lazy evaluation
• Arguments to functions are suspended as "thunks" in the heap until they are needed for:
  • primitive operations (+, -, *, etc.)
  • case, if, pattern matching

Lazy evaluation of average

  avg [1,2,3]
= worker [1,2,3] (0,0)
= worker [2,3] (1+0,1+0)
= worker [3] (2+1+0,1+1+0)
= worker [] (3+2+1+0,1+1+1+0)
= (3+2+1+0) / fromInt (1+1+1+0)
= 6 / 3
= 2.0

• Actual computation is delayed until the final operation
• For a list of length \(n\) builds up two thunks of size \(O(n)\): \(n+n-1+\cdots+1+0\) and \(1+1+\cdots+1+0\)

Eager evaluation of average

  avg [1,2,3]
= worker [1,2,3] (0,0)
= worker [2,3] (1+0, 1+0)
= worker [2,3] (1, 1)
= worker [3] (2+1,1+1)
= worker [3] (3, 2)
= worker [] (3+3,1+2)
= worker [] (6, 3)
= 6 / 3
= 2.0

Optimizing lazy evaluation

• Eager and lazy always yield the same result if both terminate
• In this example could use eager evaluation to avoid the excessive space use
• An optimizing compiler can use strictness analysis to perform this optimization
  • depends on the "cleverness" of the analysis
• Instead we can explicitly control evaluation order:
  • using the seq or the BangPatterns extension
  • this does not depend on optimizations
  • ensures performance is predictable

Controling evaluation

The primitive function seq function allows controlling evaluation order.

seq :: a -> b -> b

Evaluation of seq x y first evaluates x and then returns y.

Controlling evaluation (1)

Using seq to force evaluation of both s and n before the tail recursive call.

avg :: [Double] -> Double
avg xs = worker xs (0,0)
  where
   worker :: [Double] -> (Double,Int) -> Double
   worker [] (s,n) = s / fromIntegral n
   worker (x:xs) (s,n)
       = s `seq` n `seq` worker xs (x+s,1+n)

Controlling evaluation (2)

Bang patterns (!) also allow forcing evaluation.

{-# LANGUAGE BangPatterns #-}

avg :: [Double] -> Double
avg xs = worker xs (0,0)
  where
   worker :: [Double] -> (Double,Int) -> Double
   worker [] (s,n)       = s / fromIntegral n
   worker (x:xs) (!s,!n) = worker xs (x+s,1+n)
              -- ^^^^^^^ "bang" patterns

Results

• The example runs in constant space with either solution
• 1 MB total memory independent of the level of compiler optimizations

Folds

Fold operations

Recall the higher-order fold operations (also called reduce) that process a list using some argument function.

https://en.wikipedia.org/wiki/Fold_(higher-order_function)

Left and right folds

foldr (+) 0 [1, 2, 3, 4, 5]
= 1 + (2 + (3 + (4 + (5 + 0))))

foldl (+) 0 [1, 2, 3, 4, 5]
= ((((0 + 1) + 2) + 3) + 4) + 5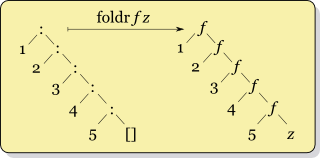

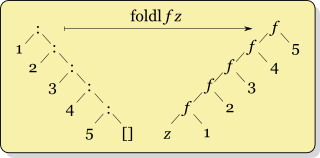
Left vs right folds

• foldr requires traversing the entire before we can start accumulating
• foldl can start accumulating immediately
• Let us express the average using a left fold

Accumulating using a left fold

We could rewrite the average example using a left fold.

avg :: [Double] -> Double
avg xs = s / fromIntegral (n :: Int)
   where (s, n) = foldl f (0,0) xs
         f (!s,!n) x = (x+s,1+n)

However, even with bang patterns, this still exhibits excessive space use!

The problem with foldl

foldl f z [] = z
foldl f z (x:xs) = f (fold f z xs) x


  foldl f z [x1, x2, x3, x4]
=
  f (f (f (f z x4) x3) x2) x1

For a list with \(n\) elements builds up a thunk f (f (...)) of \(n\) applications of the function \(f\).

A strict left fold

To avoid building up the large thunk we should to use foldl' (from Data.List):

foldl' f z [] = z
foldl' f z (x:xs) = let z' = f z x
                    in z' `seq` foldl' f z' xs

foldl' forces evaluation of f before each recursive call.

Constant-space average

import Data.List (foldl')

avg :: [Double] -> Double
avg xs = s / fromIntegral (n :: Int)
   where (s, n) = foldl' f (0,0) xs
         f (!s,!n) x = (x+s,1+n)

Note the we also need the bang patterns (!).

Reasoning about space usage

Reasoning about space usage

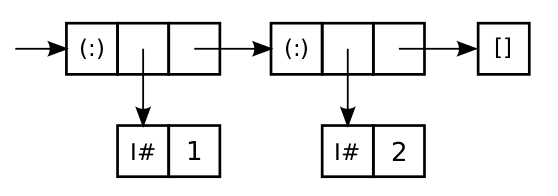
Knowning how GHC represents values in memory is useful

• allows us to approximate memory usage
• allows us to count number of indirections which affect cache behavior

Memory layout

GHC represent the list [1,2] = 1 : (2 : []) as

• Each cell represents one machine word
• Arrows represent pointers
• Each constructor has one word overhead (e.g. tag)

Memory usage for constructors

• Rough estimate: each constructor uses 1 word for a header and 1 word for each field.

   data T a b = C1 a | C2 a b
   -- C1 takes 2 words; C2 takes 3 words

• Exception: constructors with zero fields (like Nothing, True or []) take zero space because they are shared among all uses.

Unboxed types

• GHC defines several unboxed types representing primitive machine types
• Convention: names of unboxed types end with #
  • e.g. Int#, Double#
• Most unboxed types take up one word
• Values of unboxed types can never be thunks
• Basic types are internally defined in term of unboxed types

   data Int = I# Int#

• Basic types such as Int are called boxed (they are stored as small "boxes" in the heap)

Quiz

data IntPair = IP Int Int

How many words are used to store a value of this type?

Answer: 7 words.

Why box basic types?

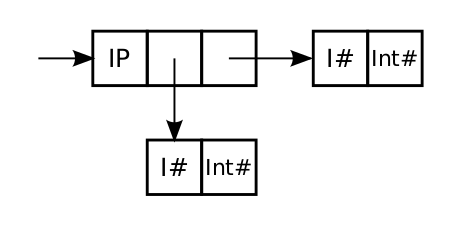
Because of lazy evaluation e.g. Int values may be thunks.

cond :: Bool -> Int -> Int -> Int
cond True x y  = x
cond False x y = y

> cond True 42 (1`div`0)
42

Unpacking

GHC allows controls over data representation using the UNPACK pragma:

• unpacks the contents of a contructor as a field of another constructor
• removes one level of indirection
• any strict, monomorphic and single constructor field may be unpacked

Add the pragma just before the strictness annotation (!):

data Foo = Foo {-# UNPACK #-} !Int

GHC will also unpack automatically if you compile with optimizations.

Example of unpacking

data IntPair = IP Int Int

data IntPair = IP {-# UNPACK #-} !Int
                  {-# UNPACK #-} !Int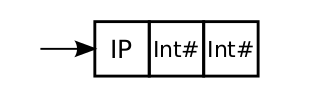

Benefits of unpacking

• Reduced allocations (3 words vs 7 for IntPair)
• Fewer indirections (allows better cache performance)

However: there are situations where making fields strict and unpacking them can hurt performance e.g. the data is passed to a non-strict function.