Bibliography

“QuickCheck: A Lightweight Tool for Random Testing of Haskell Programs” Koen Claessen and John Hughes (ICFP’2000).

Web site:

http://www.cse.chalmers.se/~rjmh/QuickCheck/

Introductory tutorial:

https://www.schoolofhaskell.com/user/pbv/an-introduction-to-quickcheck-testing

What is QuickCheck?

• A library for random-testing of Haskell programs
• The programmer writes properties rather than specific tests
• A property is an assertion that should hold for many (possibly infinite) cases
• QuickCheck tests properties with randomly-generated data

Using QuickCheck

Example

import Test.QuickCheck

prop_rev_rev :: [Int] -> Bool
prop_rev_rev xs = reverse (reverse xs) == xs

Ask GHCi to check this with randomly generated lists:

Main> quickCheck prop_rev_rev
OK, passed 100 tests.

Counter-examples

If the property fails, then QuickCheck prints out a counter-example.

import Test.QuickCheck

prop_wrong :: [Int] -> Bool
prop_wrong xs = reverse xs == xs 


Main> quickCheck prop_rev_id
*** Failed! Falsifiable
    (after 6 tests and 6 shrinks):
[0,1]

Writing properties

• Simple properties are just boolean functions
• Convention: names start with prop_
• Parameters are implicitly quantified universally
  (e.g. “for all \(xs\) assertion”)
• Polymorphic functions should be restricted to a specific type

prop_rev_rev :: [Int] -> Bool
prop_rev_rev xs = reverse (reverse xs) == xs

Means \[ \text{reverse}~(\text{reverse}~ xs) = xs, \quad \forall xs :\hspace{-0.1ex}: [\text{Int}] \]

Conditional properties

insert :: Ord a => a -> [a] -> [a]
insert x [] = [x]
insert x (y:ys)
   | x<y       = x:y:ys
   | otherwise = y:insert x ys

We want to specify that insertion preserves ordering, i.e.

\[ ordered~xs \implies ordered~(insert~x~xs), \quad \forall x, xs \]

The operator ==> allows expressing such conditional properties.

Conditional properties (2)

prop_ins_ord :: Int -> [Int] -> Property
prop_ins_ord x xs
  = ordered xs ==> ordered (insert x xs)

-- NB: the result type is now Property
-- auxiliary definition
-- to test if a list is in ascending order
ordered :: Ord a => [a] -> Bool
ordered (x:y:xs) = x<=y && ordered (y:xs)
ordered _        = True

Testing it out

> quickCheck prop_ins_ord
*Main Data.List> quickCheck prop_ins_ord 
*** Gave up! Passed only 72 tests.

What happened?

• ==> discards test cases that do not satisfy the precondition
• Fewer than 100 test cases passed this test
• QuickCheck gave up trying to generate more cases
• Did we test enough cases?

Showing test cases

We can use verboseCheck to show the actual test cases:

Main> verboseCheck prop_ins_ord
Passed:
1
[]
Skipped (precondition false):
-1
[1,-2]
....

This too verbose; it is better to collect statistical data on test cases.

Collecting data

prop_ins_ord :: Int -> [Int] -> Property
prop_ins_ord x xs
  = collect (length xs) $
    ordered xs ==> ordered (insert x xs)

Collecting data (2)

Main> quickCheck prop_ins_ord
*** Gave up! Passed only 75 tests:
38% 0
29% 2
25% 1
 4% 4
 2% 3

38% were the empty list

25% were single element lists

29% were two element lists

Only 6% were 3 or 4 elements!

Problem with conditional properties

• Most randomly-list generated lists of larger sizes are not ordered
• The pre-condition biases the test cases towards small lists
• This means that our testing did not cover enough “interesting” cases

Quantified properties

A better approach: explicitly restrict test cases using a generator:

forAll generator $ \pattern -> property

NB: this forAll is just a function defined in the QuickCheck library.

Quantified properties (2)

For our example we can use a generator called orderedList for lists of values in ascending order (also defined in the library):

prop_ins_ord2 :: Int -> Property
prop_ins_ord2 x
   = forAll orderedList $ 
     \xs -> ordered (insert x xs)

Quantified properties (3)

Using custom generator ensures better distributed test cases.

prop_ins_ord2 x =
   forAll orderedList $ \xs ->
   collect (length xs) $ 
   ordered (insert x xs)

Main> quickCheck prop_ins_ord2
 6% 0
 5% 1
 4% 32
 4% 22
 4% 2
...

Writing Generators

The Gen monad

• QuickCheck exports some basic generators and combinators for building new ones
• Gen T is the type for generators of values of type T
• Gen is a monad (and applicative functor)
• Hence: we can use do-notation or applicative operators for defining generators
• Internally, the Gen monad hides:
  • a seed for generating pseudo-random numbers
  • a size measure for controlling the size of data structures (e.g. the length of lists)

Basic generators

choose :: Random a => (a,a) -> Gen a
          -- random choice from interval
elements :: [a] -> Gen a
          -- random choice from list

Examples:

dice :: Gen Int
dice = choose (1,6)

vowel :: Gen Char
vowel = elements "aeiouAEIOU"

Combining generators

-- using do-notation
sum_dice :: Gen Int
sum_dice = do d1 <- dice
              d2 <- dice
              return (d1+d2)

-- using applicative operators
sum_dice :: Gen Int
sum_dice = (+) <$> dice <*> dice

Sampling generators

We can use sample to show random samples of a generator.

Main> sample sum_dice
3
7
8
4
8
7
5
6
2
3
6

Combinators

oneof     :: [Gen a] -> Gen a
          -- uniform random choice
frequency :: [(Int,Gen a)] -> Gen a
          -- random choice with frequency

Examples:

fruit = elements ["apple", "orange", "banana"]
sweet = elements ["cake", "ice-cream"]

-- fruit and sweets equally probable
desert = oneof [fruit, sweet] 
-- healthy option: 4/5 fruits, 1/5 sweets
healthy = frequency [(4,fruit),(1,sweet)]

Samples

Main> sample healthy
"orange"
"ice-cream"
"apple"
"banana"
"ice-cream"
"apple"
"apple"
"banana"
"orange"
"banana"
"orange"

Custom generators

We can write a custom generator using basic combinators and do-notation.

data Person = Person String Int 

genPerson :: Gen Person
genPerson =
   do name <- elements ["Alice", "Bob",
                        "David", "Carol"]
      age <- choose (10, 99)
      return (Person name age)

Samples

Main> sample genPerson 
Person "Alice" 77
Person "David" 87
Person "Alice" 67
Person "Bob" 51
Person "David" 91
Person "David" 36
Person "Alice" 47
Person "Alice" 84
Person "Carol" 36
Person "Bob" 94

List generators

listOf :: Gen a -> Gen [a]
   -- lists of random length

listOf1 :: Gen a -> Gen [a]
   -- non-empty lists of random length

vectorOf :: Int -> Gen a -> Gen [a]
   -- list of the given length

Example

Main> sample (vectorOf 5 $ elements "aeiou")
"ueuuo"
"aioua"
"iouui"
"iaoue"
"aeaii"
"iiuio"
"uuaoe"
"ieeue"
"ouiei"
"uoeoo"
"ueaeo"

Default generators

We can specify a default generator for a type in the Arbitrary class.

class Arbitrary a where
    arbitrary :: Gen a

QuickCheck defines Arbitrary instances for many basic types:

instance Arbitrary Int 
instance Arbitrary Bool
instance Arbitrary a => Arbitrary [a]
instance (Arbitrary a,
          Arbitrary b) => Arbitrary (a,b)
...

Defining a default generator

We can define instances of Arbitrary for new types:

instance Arbitrary Person where
    arbitrary = genPerson

genPerson :: Gen Person
genPerson = ... -- as before

Sized generators

Sizes of test data

• QuickCheck begins by generating “small” test data, gradually increasing a size parameter.
• The meaning of the size parameter is data-dependent, e.g.: - is the length for lists - is the magnitude for Int and Integer - ignored for enumerations (e.g. Bool or Char);
• We can use the sized combinator to access the size parameter when writing generators of recursive data structures:

  sized :: (Int -> Gen a) -> Gen a

Example: binary trees

data Tree a = Branch a (Tree a) (Tree a)
            | Leaf

Generate balanced trees

instance Arbitrary a => Arbitrary (Tree a) where
    arbitrary = sized genTree

-- | generate a tree of given size
-- size ~ number of branch nodes
genTree :: Arbitrary a => Int -> Gen (Tree a)
genTree size
  | size>0 = do v <- arbitrary
                l <- genTree (size`div`2)
                r <- genTree (size`div`2)
                return (Branch v l r)
  | otherwise = return Leaf 

Alternative (unbalanced trees)

-- size ~ upper bound of inner nodes
genTree' :: Arbitrary a => Int -> Gen (Tree a)
genTree' size
  | size>0 = frequency [(4, genBranch),
                        (1, return Leaf)]
  | otherwise = return Leaf
  where
    genBranch = do v <- arbitrary
                   l <- genTree' (size`div`2)
                   r <- genTree' (size`div`2)
                   return (Branch v l r)

Shrinking

Simplifying counter-examples

• A property fails if QuickCheck finds a counter-example
• However: randomly-generated data typically contains a lot of “noise”
• Therefore it is a good idea to simplify the counter-example before reporting them
• This is called shrinking in QuickCheck

Shrinking by example

prop_wrong :: [Int] -> [Int] -> Bool
prop_wrong xs ys =
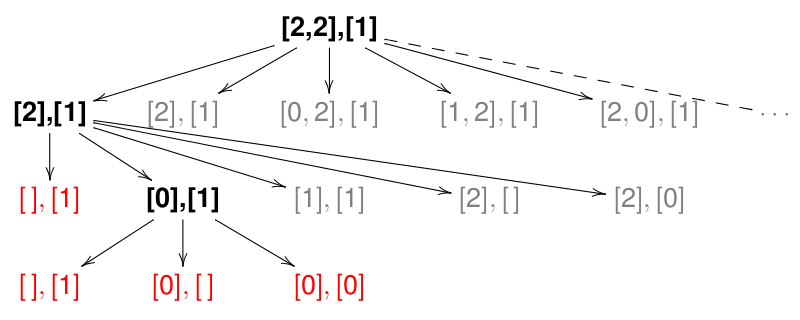
  reverse (xs++ys) == reverse xs ++ reverse ys

QuickCheck randomly generates a counter-example, e.g. xs = [2,2] and ys = [1].

Shrinking tries to find a smaller counter-example recursively:

• taking sub-lists of xs and ys;
• shrinking the values inside the list.

This process is iterated until no smaller counter-example is found.

Shrinking by example

We get xs=[0], ys=[1] after two shrinking steps; more shrinking does not yield counter-examples (local minimum).

The shrink function

The shrinking function is defined in the Arbitrary type class.

class Arbitrary a where
   arbitrary :: Gen a -- generator
   shrink :: a -> [a] -- shrink function
   shrink _ = []      -- default: no shrinking

shrink should give a (finite) list of “smaller” values to test for counter-examples.

The default gives an empty list — i.e. shrinking is disabled.

Example: binary trees

data Tree a = Branch a (Tree a) (Tree a)
            | Leaf 

Heuristic to shrink a branching node:

• replace it by a leaf;
• replace it by the left or right sub-trees;
• shrink the left or right sub-trees;
• shrink the value.

No further shrinking when we reach a leaf.

Shrinking binary trees

instance Arbitrary a => Arbitrary (Tree a) where
   arbitrary = ... -- as before
   shrink = shrinkTree

shrinkTree :: Arbitrary a => Tree a -> [Tree a]
shrinkTree (Branch v l r) =
    [Leaf, l, r] ++
    [Branch v l' r | l'<-shrinkTree l] ++
    [Branch v l r' | r'<-shrinkTree r] ++
    [Branch v' l r | v'<-shrink v]
shrinkTree _ = []  -- no shrinking for leaves

Termination

• The shrink function should reduce a value by a single step
• QuickCheck will keep applying the shrink function until it cannot find a smaller counterexample
• This will terminate if there are no infinite descending chains \(v_0\) shrinks to \(v_1\) shrinks to \(v_2\) etc.
• In practice: it is important to ensure that a value does not shrink to itself!

A larger example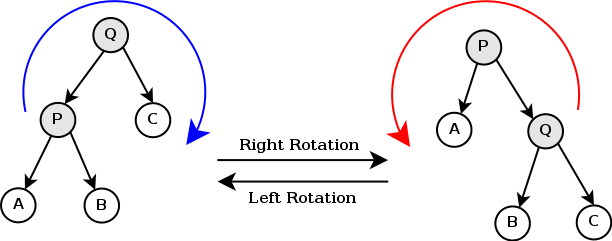

• Rotations are used in re-balancing algorithms for search trees (e.g. AVL trees, Red-Black trees)
• Property: rotations should preserve the order of values in the tree

Tree rotations

rotateL, rotateR :: Tree a -> Tree a 
rotateL (Branch x t1 (Branch y t2 t3)) 
    = Branch y (Branch x t1 t2) t3
rotateL t = t   -- nothing to do

rotateR (Branch x (Branch y t1 t2) t3) 
    =  Branch x t1 (Branch y t2 t3) 
rotateR t = t   -- nothing to do

QuickCheck properties

prop_rotateL :: Tree Int -> Bool
prop_rotateL t
   = toList t == toList (rotateL t) 
 
prop_rotateR :: Tree Int -> Bool
prop_rotateR t
   = toList t == toList (rotateR t) 

-- list tree values in order
toList :: Tree a -> [a]
toList Leaf = []
toList (Branch v l r)
    = toList l ++ [v] ++ toList r

Testing it

*Main> quickCheck prop_rotateL 
+++ OK, passed 100 tests.
Main> quickCheck prop_rotateR 
*** Failed! Falsifiable
    (after 3 tests and 3 shrinks):
Branch 1 (Branch 0 Leaf Leaf) Leaf

We found an error!

• rotateR is incorrect (x and y are switched around)
• Because of shrinking, QuickCheck found a minimal counter-example

Tips

Using newtypes

Using newtype allows customizing the generators for specific uses.

data Expr = Var String | ...

vs.

data Expr = Var Name | ...
newtype Name = Name String

instance Arbitrary Name where
    arbitrary = do n<-elements ["a","b","c","d"]
                   return (Name n)

Newtypes in the library

newtype NonNegative a = NonNegative a
newtype NonZero a = NonZero a
newtype Positive a = Positive a
newtype NonEmptyList a = NonEmpty [a]
newtype OrderedList a = Ordered [a]

Allow restricting the range of generated values:

prop_add (Positive x) y = x+y > y
   where types = (x::Integer,y::Integer)

prop_len (NonEmpty xs) = length xs > 0
   where types = xs :: [Int]