[AED 14] Nós por nível de profundidade

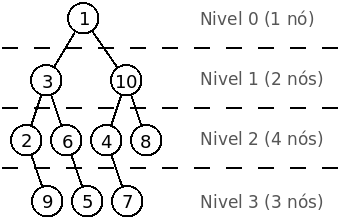
Dada uma árvore binária, a tua tarefa é descobrir quantos nós existem em cada nível de profundidade. Recorda que a profundidade de um nó é o tamanho do caminho entre a raíz e esse nó (onde o tamanho do caminho é o número de arestas percorridas). A seguinte imagem ilustra uma árvore binária e o número de nós em cada nível de profundidade.

Input

Na primeira linha do input vem um inteiro T indicando o número de casos de teste, ou seja, o número de árvores a considerar a considerar.

Cada árvore é indicada por duas linhas:

• A primeira linha indica o número de nós N da árvore. Cada nó é identificado por um número distinto entre 1 e N e o nó 1 é sempre a raíz da árvore.
• A segunda linha contém N-1 nós, indicando os pais (antecessores) de cada nó. O i-ésimo número da linha indica o pai do nó i+1 (o primeiro número indica o pai do nó 2, o segundo número indica o pai do nó 3, etc).

É garantido que as árvores são binárias (existem no máximo dois filhos em cada nó). Note também que a maneira como é dado o input não lhe garante conseguir distinguir qual é o filho esquerdo e o filho direito, mas para este problema essa distinção não é realmente necessária, pois não?

Output

O output deve conter T linhas. A i-ésima linha deve indicar o número de nós em cada nível da árvore correspondente. Estes devem vir por ordem de nível (do nível 0 para o nível mais profundo) e deve ser separados por um espaço (nota que não deve vir um espaço a mais no final da linha).

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

Exemplo de Input

2
10
3 1 10 6 3 4 10 2 1
4
4 4 1

Exemplo de Output

1 2 4 3
1 1 2

Explicação do Input/Output

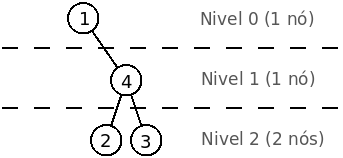
O primeiro caso do exemplo de input corresponde à árvore dada em cima no enunciado. O segundo caso corresponde à árvore da figura em baixo.

Algoritmos e Estruturas de Dados (L.EIC011)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto
DEI/FEUP - Faculdade de Engenharia da Universidade do Porto