In what concerns the continuous evaluation solving exercises during the semester, the exercises you can submit in this class are:
Submission Deadline: October 19th (submit to AED's Mooshak)
You are encouraged to talk to the professor and to your colleagues if you have difficulties. However, any more direct help you have received from other colleagues should be acknowledged in the comments of the code you submit.
After the deadline the problems will still be available on Mooshak, but the submissions will not count towards your grade.
Each class is worth 10 per cent of the grade for this component. As there will be 11 classes with submissions, you can get full marks even if you haven't done everything.
For a problem to count, you have to get all the tests right (i.e. accepted). Even if you solve all the problems, the maximum in a single class is 100 per cent.
it is guaranted that the main exercises on each class will sum to at least 100% of the class grade.
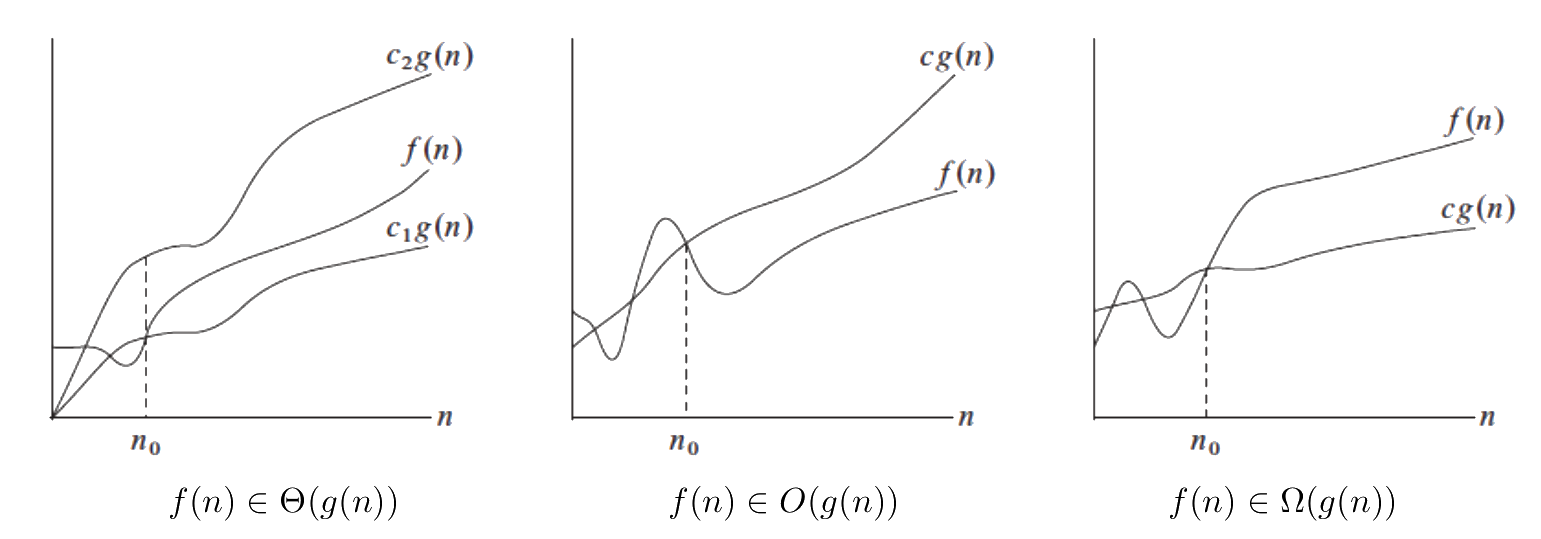
This class is about complexity and asymptotic analysis. It is therefore convenient that you know what was discussed on the lectures:
Recall that:

1. Explain why each statement is true, using the definition of the classes \( O(\cdot) \), \( \Omega(\cdot) \) and \( \Theta(\cdot) \).
2. Justify the truthfulness or falsity of each statement.
3. Characterize the asymptotic time complexity of the function remove, where the array x has at least \(n\) elements. Describe what characterizes best case and worst case instances.
int remove(int x[], int n, int v) { int t = 0; for (int j=0; j<n; j++) if (x[j] <= v) x[t++] = x[j]; return t; }
4. Characterize the asymptotic time complexity of the function symmetric, where x is a square matrix defined with \( \mathtt N \) columns at most, and \(1 \leq \mathtt n\leq \mathtt N\). Describe best case and worst case instances.
bool symmetric(int x[][N], int n) { for (int i=1; i < n; i++) for(int j = 0; j < i; j++) if (x[i][j] != x[j][i]) return false; return true; }
5. Characterize the asymptotic time complexity of the function product, where x, y and z square matrices (all of the same dimension \(n\)), defined with \(\mathtt N\) columns at most, and \( 1 \leq \mathtt n \leq \mathtt N\). Describe best case and worst case instances.
void product(int x[][N], int y[][N], int z[][N], int n) { for (int i=0; i < n; i++) for(int j = 0; j < n; j++) { z[i][j] = 0; for(int k = 0; k < n; k++) z[i][j] += x[i][k]*y[k][j]; } }
6. Characterize the asymptotic time complexity of my_3SUM, as a function of the size of vector x. Describe best case and worst case instances.
#include <iostream> #include <vector> using namespace std; bool my_3SUM(const vector<int> & x) { int n = x.size(); for (int i=0; i < n-2; i++) for(int j = i+1; j < n-1; j++) for(int k = j+1; k < n; k++) if (x[i]+x[j]+x[k] == 0) { cout << i << ' ' << j << ' ' << k << endl; return true; } return false; }
7. Assume that v and w are vectors and both contain a sequence of nonnegative integers that ends with 0 (and has no other zeros). Let \(a_1, a_2,\ldots, a_m,0\) and \(b_1,b_2,\ldots, b_n,0\) be such sequences, with \(m\geq 1\) and \(n\geq 1\). The function returns an integer which is either positive, negative or 0, if the sequence given by v is lexicographically greater than, less than or equal to the sequence given by w, respectively. Recall that all \(a_i\)'s and \(b_i\)'s are positive integers.
int lex_comp(const vector<int> &v, const vector<int> &w) { int j = 0; while (w[j] == v[j] && v[j] != 0) j++; return v[j]-w[j]; }
8. Recall the problem \(\mathtt{Partition}\) which, given a set \(S=\{a_1,a_2,\ldots, a_n\}\) of \(n\) positive integers, asks whether there is a set \(A\subset S\) such that \(\sum_{x\in A} x = \sum_{x \in S\setminus A} x\). The following function solves the problem when we call search(x,0,n,0,0,res,nres), with nres=0, and x and res being arrays with at least \(n\geq 2\) elements. In addition, it returns a set \(A\) in res. It implements a brute force search algorithm.
bool search(int x[],int i, int n, int s, int r, int res[], int & nres) { if (i == n) return s == r; s += x[i]; res[nres++] = i; if (search(x,i+1,n,s,r,res,nres)) return true; s -= x[i]; nres--; r += x[i]; return search(x,i+1,n,s,r,res,nres); }
9. My first Mooshak submissions

On this course we will use Mooshak to automatically evaluate your C++ code (see Mooshak's help).
To access the system you can use your login (with the word "up")
and password that was sent to your institutional email (message sent on the 30th of September with the title "[AED] Mooshak password - login")
(if you have trouble accessing it, send a message on discord to @PedroRibeiro)
In this problem the goal is to make your first submissions in Mooshak, all for the [AED000] This is not a problem!. The problem statements will also be available inside Mooshak. Always start by carefully reading the problem statement given!
10. My first Mooshak problem in which efficiency matters

For this exercise you will be solving the problem [AED001] Prime Numbers.
11. Maximum Subarray Sum

For this exercise you will be solving the problem [AED002] Sequence Game.
The goal of this exercise is to produce algorithms with different time complexities and check their efficiency when submitting. You should start by carefully reading the problem statement.
What are all the possible contiguous subsequences? Let v be a vector containing the sequence and \(n\) its length. The possible sequences are therefore all the subsequences \(v[i \dots j]\) such that \(0 \leq i \leq j \lt n\).
An exhaustive "brute force" would be to go through all the subsequences and for each of them compute the respective sum, choosing the best possible sum.
Supposing we already read the input to a vector v, a way of doing this would be calling the following the following maxSum function that returns the best sum:
int maxSum(const vector<int> &v) { int n = v.size(); int maxSoFar = v[0]; // why is this a good choice for the best initial sum? for (int i=0; i<n; i++) // all possible initial positions for (int j=i; j<n; j++) { // all possible final positions int sum = 0; for (int k=i; k<=j; k++) // compute sum between positions i and j sum += v[k]; if (sum > maxSoFar) maxSoFar = sum; } return maxSoFar; }
Understand what the code above does, implement the rest of the code (reading the input and calling the function) and submit it to Mooshak. See how many tests this code passes and why it fails on the bigger tests (remember you can click on the result to see detailed feedback on the submission).
Intuitively, looking at the previous code, we can note we are repeating to many calculations. When we go from from \(sum(v[i \ldots j])\) to \(sum(v[i \ldots j+1])\) we do not need to recompute everything (starting again at position \(i\)), and we can just add \(v[j+1]\) to the previous sum.
In other words, \(sum(v[i \ldots j+1]) = sum(v[i \ldots j]) + v[j+1]\). We can use this to remove the third cycle with \(k\) that we had on our previous solution..
Implement this new solution and submit it. Can you see you now passed in more tests? Why? But we still need to improve to have an accepted solution...
A quadratic solution is still not enough and need to improve it to linear time. For that we will use Kadane's algorithm.
Considere that \(best(i)\) represents the best subsequence that ends on position \(i\). We know as a base case that \(best(0) = v[0]\) (it's the only possible subsequence that ends on the first position).
If we know how to compute \(best(i)\), how can we compute the value of \(best(i+1)\)?
| \(i\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(v[i]\) | 4 | -2 | 1 | 5 |
| \(best(i)\) | 4 | 2 | 3 | 8 |
\(best(2) = 3\), obtained with the subsequence \([4,-2,1]\).
\(best(3) = best(2) + v[3] = 3 + 5 = 8\), obtained with the subsequence \([4,-2,1,5]\) (we extend the previous subsequence).
| \(i\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(v[i]\) | -5 | 2 | -3 | 4 |
| \(best(i)\) | -5 | 2 | -1 | 4 |
\(best(2) = -1\), obtained with the subsequence \([2,-1]\).
\(best(3) = v[3] = 4\), obtido através do subarray \([4]\) (we did not extended the previous subsequence).
At the end, the best sum is the maximum value of \(best(i)\) for any possible \(i\) (the best subsequence can terminate in any position).
To compute this we can traverse only once the vector v and in each iteration compute in constant time the value of the best sum terminating on the current position using the best sum terminating on the previous position. The temporal complexity of this approach is linear.
Implement this solution, submit and verify it passes all test cases, obtaining your deserved Accepted 🙂
AED Mooshak classes will usually include at least one extra exercise that you can use of you want to keep testing your knowledge of the material. For this class we propose another problem for which temporal efficiency is needed and the exhaustive "brute force" solution is not enough.

For this exercise you will be solving the problem [AED003] Saving Pipefish.
This exercise is an adaptation of a problem that was the easiest one on the qualification for a past National Olympiads in Informatics qualification phase, an high-school algorithmic contest.
A "brute force" solution that tries all possible sections and for each of them tests all positions to see how many of them are larger than \(T\) is not enough, since it would spend \(N^2\) time (can you see why? imagine a case with \(K=N/2\)). We need a better solution...
(click to see hints; try to solve the problem first if you do not want spoilers)
- Imagine you already processed the section \([a,b]\), having obtained \(Q_a\), the amount of elements larger or equal than \(T\) in that section.
- The next section is \([a+1,b+1]\). What changes in that interval? Only the position \(a\) is removed and the position \(b+1\) is inserted. The (new) value of \(Q_{a+1}\) is therefore equal to \(Q_a\), subtracting 1 in case the depth of position \(a\) is \(\ge T\) and adding 1 in case the depth of position \(b+1\) is \(\ge T\).
- For each new interval we only need to make a constant number of operations (considering the element to remove and the element to insert).
Regarding efficiency this corresponds to an initial cycle for the first section of size \(K\) and for the remaining \(N-K\) sections we spend constant time. Another way of reasoning about this is that each position is added only once to the current section, and removed once from it. This is therefore a solution in time \(\Theta(N)\) obtaining the desired Accepted results.
- This idea of reusing the result of the previous section to compute the result of the next one is known as the sliding window technique, since we are "sliding" the windows of the current section along the input.
AED Mooshak classes will usually include one challenge exercise, which can be much harder the previous ones and might even need knowledge that was not given explicitly on the course.
The main idea is to give you the opportunity of improving your problem solving abilities.

For this exercise you will be solving the problem [AED004] Number Spiral.
Because this is the first challenge, the selected problem is not too hard and can be solved by any student without any knowledge of advanced algorithms or data structures. You just need to think a little bit and of course go beyond the naive "brute force" approach 😉
Since this is a challenge, I will not give you any hints, but if you are stuck just contact @PedroRibeiro on Discord. Feel free to also contact @PedroRibeiro to discuss your accepted solution.
Happy coding! 😊