Practical Class #12 - Priority Queues and Heaps
(16/12 to 20/12)
Exercises for submission
In what concerns the continuous evaluation solving exercises during the semester, the exercises you can submit in this class are:
Submission Deadline: January 4th (submit to AED's Mooshak)
You are encouraged to talk to the professor and to your colleagues if you have difficulties. However, any more direct help you have received from other colleagues should be acknowledged in the comments of the code you submit.
After the deadline the problems will still be available on Mooshak, but the submissions will not count towards your grade.
Each class is worth 10 per cent of the grade for this component. As there will be 11 classes with submissions, you can get full marks even if you haven't done everything.
For a problem to count, you have to get all the tests right (i.e. accepted). Even if you solve all the problems, the maximum in a single class is 100 per cent.
it is guaranted that the main exercises on each class will sum to at least 100% of the class grade.
Lectures Content
This class is about Priority Queues and heaps. It is therefore convenient that you know what was discussed on the lectures:
1. Understanding Priority Queues and Heaps
A priority queue ADT (abstract data structure) maintains a collection of elements allowing for efficient insertion removal of the highest priority element (let's assume for the purposes of this exercise that the highest priority is the largest).
One way to implement priority queues with efficient operations in logarithmic time is to use a special type of trees called binary heaps. In a (max) heap, any node must always be greater (or equal) than its children (meaning that the largest of all is at the root). Furthermore, a heap is a complete tree (all levels full, except potentially the last one, with the nodes placed as far to the left as possible - which implies that it is balanced and has height \(\mathcal{O}(\log n)\). A heap typically implemented using an array (where the node at position \(i\) has as its children the nodes at positions \(i \times 2 \) and \( i \times 2 + 1\).
The way a heap works was explained in the lectures: 14 - Priority Queues [slides 7 to 13]
- Visualizing Heaps
Use the following page to interact and visualize heaps, experimenting at least with several insertions (Insert(v)) and removals (ExtractMax()), trying to understand what's happening and how heaps work:
VisuAlgo - Binary Heap
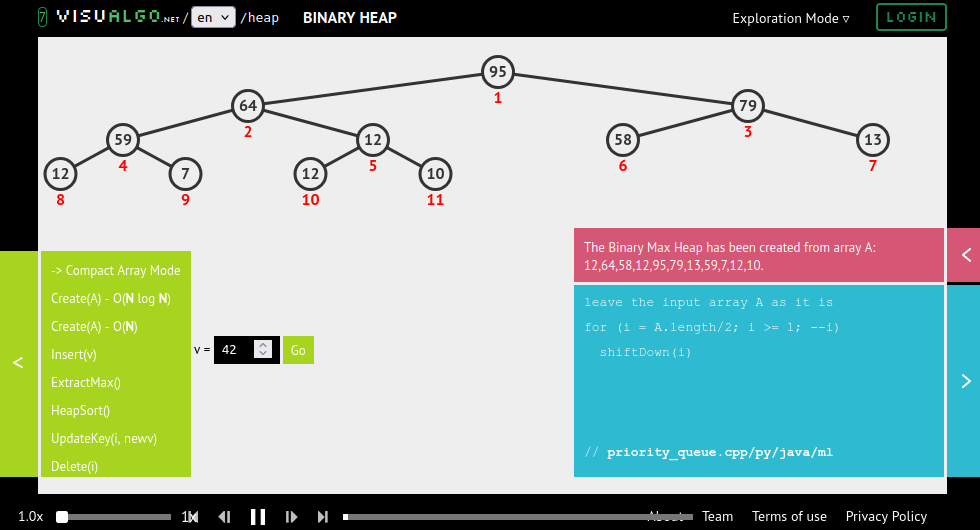
- A (simple) heap implementation
Download the following two files: maxHeap.h (see it in html) and testHeap.cpp (see it in html) with the max heap implementation explained in the lectures. [slides 20 to 27]
Compile and execute the code. The whole MaxHeap<T> class is contained in the .h file, so you just need to compile testHeap.cpp (make sure they are in the same directory, so that the line #include "maxHeap.h" knows where to find the file it wants to include). If you are on a shell, you could for instance run g++ -std=c++17 -o testHeap testHeap.cpp to obain an executable with the name testHeap).
Running the code you should obtain the following as the output:
h.max() = 91
91 83 71 61 53 42 37 23 17 9
h.max() = -1
Experiment a bit with the code. For instance, can you create a heap of strings, populate it and then remove one by one to see the order in which the elements come out?
2. A first problem with heaps

For this exercise you will be solving the problem [AED072] Is this a Heap?.
Desired time complexity: \(O(L)\) (for each array, where L is its length)
This exercise is designed to make sure you understand the heap invariant (the parent has always higher priority than its children) and that you understand how to access the children nodes when the heap is stored as as array.
It is pretty straightforward and you just need to do what is asked 😉
Hints
- Just traverse each element on position i of the respective array and check if its children, if they exist (positions i*2 and i*2+1 are always smaller or equal than the parent to see if it's a max heap (or greater or equal than the parent for the min heap).
- Be careful with the case where all elements are the same (it is both a max and a min heap).
3. Using Heaps with integers

For this exercise you will be solving the problem [AED073] Rope Connections.
Desired time complexity: \(O(N \log N)\) (where N is the number of ropes)
Can you devise a greedy strategy where you end up having the minimum cost? Which should be the initial choice? And after that?
For this problem we suggest you use the available C++ priority_queue (see [slides 28 to 32] for an example usage).
Hints
- Always choose the two minimum length ropes available until you have only one rope
- To implement this efficiently, keep a priority_queue q with all the ropes:
. At the beginning insert all rope length in q
. Keep removing the two smallest lengths l1 and l2 from q and reinsert l1+l2 in q (adding l1+l2 to the cost)
- Since C++ has max heaps and here you want minimum length you can for instance... keep on the queue the negative versions of the lengths!
(you can also use a custom comparator - C++ already has a comparator that can be used to have a min heap)
4. Using Heaps with persons (that have a name and a priority)

For this exercise you will be solving the problem [AED074] Highest Bidder.
Desired time complexity: \(O(N \log N)\) (where N is the number of events)
Can you think on how priority queues will be helpful for this problem?
For this problem we suggest you use the available C++ priority_queue (see [slides 28 to 32] for an example usage).
Hints
- Just keep a priority_queue with all the current offers
- Anytime there is a sale, remove the highest offer from the queue
- Since you need to know the name of highest bidder, you can for instance have a priority_queue of pairs <intr,string> (which will use the first element of the pair when comparing elements, effectively using the price offered has the priority)
Extra Exercises for Consolidating your knowledge [extra]
5. Simulation and Priority Queues

For this exercise you will be solving the problem [AED075] Space Tourism.
Desired time complexity: \(O(N \log N)\) (where N is the number of clients)
For this problem we suggest you use the available C++ priority_queue (see [slides 28 to 32] for an example usage).
Hints
Can you do this one by yourself? 😊
Challenges Exercises [challenge]
The main idea of the challenge problems is to give you the opportunity of improving your problem solving abilities.

For this exercise you will be solving the problem [AED076] (More) Alien Words.
This problem is an extension of the challenge problem for the previous class... now the alien words can be bigger than 5 letters!
Since this is a challenge, I will not give you any more hints for now, but if you are stuck just contact @PedroRibeiro on Discord. Feel free to also contact @PedroRibeiro to discuss your accepted solution.
Happy coding! 😊
