In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of December 7th
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #08 exercise sheet]

[AED045] Node Balance

In this problem you should only submit a binarySearchTree.h file with a self-containing definition of a class BinarySearchTree<T>

Base Code

Use as a basis the class BinarySearchTree<T> (see code | download code) which implements a generic binary search tree that was given in the classes, with methods to read insert, remove and check of a value exists, to write a preOrder traversal with N as null nodes and the number of nodes and height of the tree.

The Problem

Add a new method int balance(const T & val) to the class. The function should return an integer containing the imbalance of the node containing the value val. The imbalance is expressed as the height of the right branch minus the height of the left branch. If the value val doesn't exist, the method should return zero.

You can be assured that there will be no repeated values in the tree.

Submission

You should submit the file binarySearchTree.h with the method balance added to binarySearchTree<T> as requested (and without removing any of the other existing methods). You can however create additional methods, if you need them.

Mooshak will use the following code to link to your class, read the inputs, build the trees and call your method, printing its result.

#include <iostream>
#include <string>

#include "binarySearchTree.h"

int main() {
  BSTree<int> t;

  // Read tree by inserting numbers
  int n;
  std::cin >> n;
  for (int i=0; i<n; i++) {
    int x;
    std::cin >> x;
    t.insert(x);
  }

  // Read queries and print their result
  int q;
  std::cin >> q;
  for (int i=0; i<q; i++) {
    int x;
    std::cin >> x;
    std::cout << "t.balance(" << x << ") = " << t.balance(x) << std::endl;    
  }
  
  return 0;
}

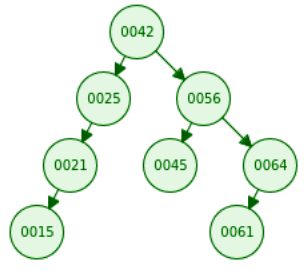
8
42 25 56 21 45 64 15 61
4
42 25 56 88

t.balance(42) = 0
t.balance(25) = -2
t.balance(56) = 1
t.balance(88) = 0

Explanation of Example Input

The tree of the example input corresponds to the following figure:

• t.balance(42) = 0, since the heights of the left and right branches of the node with 42 are the same
• t.balance(25) = -2, since the height of the right branch is -2 when compare to the left branch of the node with 25.
• t.balance(56) = 1, since the height of the right branch is +2 when compare to the left branch of the node with 56.
• t.balance(88) = 0, since the value 88 is not on the tree.