In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of December 21st
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #10 exercise sheet]

[AED062] Shortest Path

In this problem you should only submit a graph.h file with a self-containing definition of a class Graph.

Base Code

Use as a basis the class Graph (see code | download code) which implements a graph (that can have directions and weights) using an adjacency list, assumes nodes are identified by integers between 1 and |V| and already has methods for adding an edge, reading a graph and doing a basic DFS and a basic BFS.

The Problem

Add a new method std::list<int> shortestPath(int a, int b) to the class. When called on an unweighted graph, the function should return a shortest path between a and node b, given as a list of sucessive nodes on path, starting with a and ending on b.

If there is no such path, the returned list should be empty. If there is more than one path, choose the path that is smaller lexicographically when starting from the end (e.g. path a₁→a₂→...→a_n is smaller lexixographically than b₁→b₂→...→b_n if a_n<b_n; in case of tie if a_n-1<b_n-1, in case of a new tie if a_n-2<b_n-2 and so on). This corresponds effectively on always choosing the smallest possible predecessor for each node on the path.

All the input graphs will be simple (no self-loops or parallel edges) and unweighted, but they can directed or undirected. It is guaranteed that |V|≤100, |E|≤500 and that the function will be called with valid nodes (i.e., 1≤a,b≤|V|) and that a will be different than b.

Submission

You should submit the file graph.h with the method shortestPath added to Graph as requested (and without removing any of the other existing methods). You can however create additional methods and/or attribute variables, if you need them.

Mooshak will use the following code to link to your class, read the inputs, build the graphs and call your method, printing its result.

#include <iostream>
#include "graph.h"

int main() {

  // Read one input graph
  Graph *g = Graph::readGraph();

  // read q pairs of integers to indicate the queries
  int q;
  std::cin >> q;
  for (int i=0; i<q; i++) {
    int a, b;
    std::cin >> a >> b;
    std::cout << "g->shortestPath(" << a << "," << b << ") =";
    std::list<int> path = g->shortestPath(a,b);
    if (path.size() == 0) std::cout << " EMPTY";
    else for (int v : path) std::cout << " " << v;
    std::cout << std::endl;
  }
  
  delete g;
  
  return 0;
}

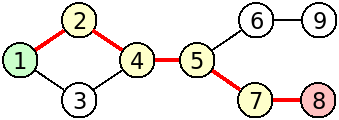
9 undirected unweighted
9
1 3
4 3
4 5
5 6
5 7
6 9
7 8
1 2
4 2
6
1 2
1 5
1 8
4 9
8 3
5 1

g->shortestPath(1,2) = 1 2
g->shortestPath(1,5) = 1 2 4 5
g->shortestPath(1,8) = 1 2 4 5 7 8
g->shortestPath(4,9) = 4 5 6 9
g->shortestPath(8,3) = 8 7 5 4 3
g->shortestPath(5,1) = 5 4 2 1

Explanation of Example Input 1

The graph of the example input 1 corresponds to the following figure:

• g->shortestPath(1,2) = 1 2, corresponding to path 1→2
• g->shortestPath(1,5) = 1 2 4 5, corresponding to path 1→2→4→5 (path 1→3→4→5 has the same distance but it is not smaller lexicographically)
• g->shortestPath(1,8) = 1 2 4 5 7 8, corresponding to path: 1→2→4→5→7→8 (path 1→3→4→5→7→8 has the same distance but it is not smaller lexicographically)
• g->shortestPath(4,9) = 4 5 6 9, corresponding to path: 4→5→6→9
• g->shortestPath(8,3) = 8 7 5 4 3, corresponding to path: 8→7→5→4→3
• g->shortestPath(5,1) = 5 4 2 1, corresponding to path: 5→4→2→1 (path 5→4→3→1 has the same distance but it is not smaller lexicographically)

8 directed unweighted
8
1 3
2 1
4 2
5 4
5 6
6 7
6 8
8 7
4
5 3
3 5
5 8
6 7

g->shortestPath(5,3) = 5 4 2 1 3
g->shortestPath(3,5) = EMPTY
g->shortestPath(5,8) = 5 6 8
g->shortestPath(6,7) = 6 7

Explanation of Example Input 2

The graph of the example input 2 corresponds to the following figure:

• g->shortestPath(5,3) = 5 4 2 1 3, corresponding to path: 5→4→2→1→3)
• g->shortestPath(3,5) = EMPTY, since there is no path from node 3 to node 5
• g->shortestPath(5,8) = 5 6 8, corresponding to path: 5→6→8
• g->shortestPath(6,7) = 6 7, corresponding to path: 6→7