In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of December 21st
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #10 exercise sheet]

[AED065] Articulation Points

In this problem you should only submit a graph.h file with a self-containing definition of a class Graph.

Base Code

Use as a basis the class Graph (see code | download code) which implements a graph (that can have directions and weights) using an adjacency list, assumes nodes are identified by integers between 1 and |V| and already has methods for adding an edge, reading a graph and doing a basic DFS and a basic BFS.

The Problem

Add a new method std::set<int> articulationPoints() to the class. When called on a connected, unweighted and undirected graph, the function should return the articulation points of the graph, given as a set of integers. An articulation point is a vertex whose removal increases the number of connected components

All the input graphs will be simple (no self-loops or parallel edges), connected, unweighted and undirected. It is guaranteed that |V|≤100 and |E|≤500.

Submission

You should submit the file graph.h with the method articulationPoints added to Graph as requested (and without removing any of the other existing methods). You can however create additional methods and/or attribute variables, if you need them.

Mooshak will use the following code to link to your class, read the inputs, build the graphs and call your method, printing its result.

#include <iostream>
#include "graph.h"

int main() {

  // Number of graphs to test
  int n;
  std::cin >> n;
  
  // For each graph: read, call the method and delete graph at the end
  for (int i=1; i<=n; i++) {
    Graph *g = Graph::readGraph(); 
    std::cout << "Graph #" << i << ":";
    std::set<int> articulation = g->articulationPoints();
    if (articulation.size() == 0) std::cout << " EMPTY";
    else for (int v : articulation) std::cout << " " << v;
    std::cout << std::endl;
    delete g;
  }
  
  return 0;
}

4
  
10 undirected unweighted
11
1 2
1 4
2 3
3 4
5 3
5 6
5 9
5 7
7 8
8 9
8 10

4 undirected unweighted
4
1 2
2 3
3 4
4 1

5 undirected unweighted
4
2 1
3 1
1 4
1 5

8 undirected unweighted
9
1 2
2 3
3 4
1 5
2 5
3 8
4 8
5 6
7 8

Graph #1: 3 5 8
Graph #2: EMPTY
Graph #3: 1
Graph #4: 2 3 5 8

Explanation of Example Input

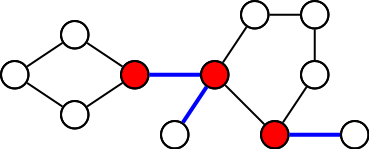
The first graph of the example input corresponds to the following figure:

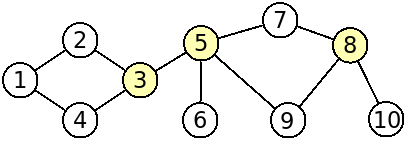
It has 3 articulation points: {3,5,8}.

The second graph of the example input corresponds to the following figure:

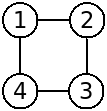
It does not have any articulation point.

The third graph of the example input corresponds to the following figure:

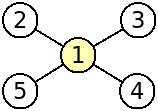
It has 1 articulation point: {1}.

The fourth graph of the example input corresponds to the following figure:

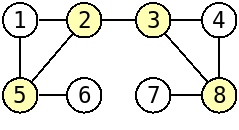
It has 4 articulation points: {2,3,5,8}.