In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of January 4th
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #11 exercise sheet]

[AED069] Hash Tables with Open Addressing

In this problem you should only submit a hashTableOA.h file with a self-containing definition of a class HashTableOA<KeyType>

Base Code

Use as a basis the skeleton code of HashTableOA<KeyType> (see code | download code) which provides the initial code for a basic implementation of an hash table using open addressing with linear probing for collision resolution and lazy deletion.

The Problem

Implement the following 3 methods (which already exist on the given file, but still lack functional code):

• bool contains(const KeyType & k) should return true if the key k exists in the hash, and false otherwise.
• bool insert(const KeyType & k) should try to insert the key k in the hash table, returning true when successful (the key was inserted) and false otherwise (the key was not inserted because it already existed or because if it would be inserted, then the table would be full - there always has to be at least one EMPTY position). The state of the bucket where the key was inserted should change to ACTIVE.
• bool remove(const KeyType & k) should try to remove the key k in the hash table, returning true when successful (the key was removed) and false otherwise (the key was not removed because it did not exist). The state of the bucket where the key was removed from should change to DELETED.

In all methods, to find the corresponding position (bucket) on the table, use modular hashing over the hash function of the class (that was initialized on the constructor), that is, for key k the position can be found calling hash(k) % size.

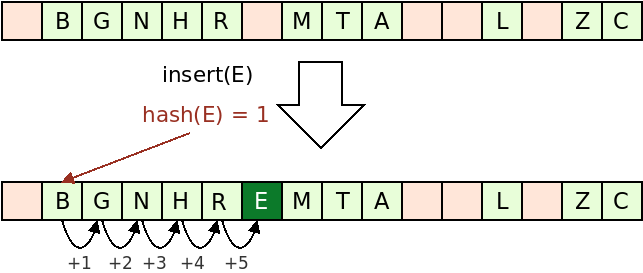
If the position is occupied, you should use linear probing, that is, go incrementally one by one over the positions (if necessary going back to the first bucket after the last bucket) until you find a bucket in the state you are looking for. A bucket can be in one of 3 states:

• EMPTY: the bucket is empty
• ACTIVE: the bucket contains a key
• DELETED: the bucket contained a key that was deleted

Deleted buckets are treated as empty when inserting (you can put a key there) and as occupied during a search for a key.

On methods insert and remove, don't forget to update the numberActive and numberDeleted variables to reflect the changes on the number of buckets that are active (contain a key) or deleted (contained a key, but was deleted).

Submission

You should submit the file hashTableOA.h with the methods contains, insert and remove implemented as requested (and without removing any of the other existing methods). You can however create additional methods, if you need them.

Mooshak will use the following code to link to your class, construct the hash table, read the operations and call your methods, printing its result.

#include <string>
#include "hashTableOA.h"

// Read hash table and then q operations
template <typename KeyType>
void read() {
  int n;
  std::cin >> n;
  std::hash<KeyType> h;
  HashTableOA<KeyType> hashTable(n, h);

  int q;
  std::cin >> q;
  for (int i=0; i<q; i++) {
    std::string op;
    KeyType k;
    std::cin >> op;
    if (op == "CONTAINS") {
      std::cin >> k;
      std::cout << "contains(" << k << "): " << hashTable.contains(k) << std::endl;
    } else if (op == "INSERT") {
      std::cin >> k;
      std::cout << "insert(" << k << "): " << hashTable.insert(k) << std::endl;
    } else if (op == "REMOVE") {
      std::cin >> k;
      std::cout << "remove(" << k << "): " << hashTable.remove(k) << std::endl;
    } else if (op == "SHOW") {
      std::cout << "showContents():" << std::endl;
      hashTable.showContents();
    }
  }
}

int main() {

  std::string type;
  std::cin >> type;
  if (type == "int") read<int>();
  else if (type == "string") read<std::string>();
  
  return 0;
}

int 5
17
INSERT 42
INSERT 39
SHOW
INSERT 17
INSERT 12
INSERT 42
CONTAINS 17
CONTAINS 52
SHOW
REMOVE 39
REMOVE 39
REMOVE 12
SHOW
INSERT 10
INSERT 20
INSERT 52
SHOW

insert(42): 1
insert(39): 1
showContents():
Size: 5 | Nr Active: 2 | Nr Deleted: 0 | Load Factor: 0.400
Table: {} {} 42 {} 39
insert(17): 1
insert(12): 1
insert(42): 0
contains(17): 1
contains(52): 0
showContents():
Size: 5 | Nr Active: 4 | Nr Deleted: 0 | Load Factor: 0.800
Table: 12 {} 42 17 39
remove(39): 1
remove(39): 0
remove(12): 1
showContents():
Size: 5 | Nr Active: 2 | Nr Deleted: 2 | Load Factor: 0.800
Table: DEL {} 42 17 DEL
insert(10): 1
insert(20): 0
insert(52): 1
showContents():
Size: 5 | Nr Active: 4 | Nr Deleted: 0 | Load Factor: 0.800
Table: 10 {} 42 17 52

Explanation of the Example Input:

On the "images", a red cell corresponds to an EMPTY bucket, a dark grey cell to a DELETED bucket and a green cell to an ACTIVE bucket.

An empty hash table is initially created with 5 buckets. Afterwards:

• 42 is successfully inserted at bucket 2
• 39 is successfully inserted at bucket 4
• The contents of the hash table are shown and correspond to the following scenario:
  

  42

  39

• 17 is successfully inserted at bucket 3 (with linear probing that started on bucket 2)
• 12 is successfully inserted at bucket 0 (with linear probing that started on bucket 2)
• 42 is not inserted (it already existed)
• contains(17) is true because 17 is on table
• contains(52) is false because 52 is not on table
• The contents of the hash table are shown and correspond to the following scenario:
  

  12

  42

  17

  39

• 39 is successfully removed from bucket 3 (with linear probing that started on bucket 2)
• 39 is not removed (it was not on the table)
• 12 is successfully removed from bucket 0 (with linear probing that started on bucket 2)
• The contents of the hash table are shown and correspond to the following scenario:
  

  DEL

  42

  17

  DEL

• 10 is successfully inserted at bucket 0
• 20 is not successfully inserted (it would use the last empty space)
• 52 is successfully inserted at bucket 4 (with linear probing that started on bucket 2)
• The contents of the hash table are shown and correspond to the following scenario:
  

  10

  42

  17

  52