[AED032] Squared Notebook

In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of November 8th
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #05 exercise sheet]

[AED032] Squared Notebook

You already know that Sarah loves her squared notebook, right? To pass the time, she began writing ainteger numbers consecutively. However, she found that doing it from left to right and top to bottom was very boring! She therefore decided to fill in the numbers diagonally using the following pattern:

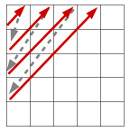
This results in the grid being filled in as shown below, where part of Sarah's notebook can be seen (the other rows and columns that do not appear in the figure are also filled in with numbers):

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

Sarah thinks it looks really cool! As her school is currently teaching addition, she decided to start adding up the numbers inside the rectangles. For example, if she considered the rectangle in the following figure (with corners at numbers 13 and 51), the sum would be equal to 358 (13+19+26+34+18+25+33+42+24+32+41+51):

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

Sarah would like to be able to check whether the sums are correct. Of course, she would like to know the sum of any given rectangle. Can you help her?

The Problem

Given a set of N rectangles, each indicated by the numbers in their corners A_i and B_i, determine the sum of the numbers contained in each rectangle, assuming that the squared notebook has been filled in by the diagonals as described above. You can assume that the notebook is so large that Sarah always has a square available when she needs to write a new number.

Input

The first line contains an integer N, indicating the number of rectangles to consider. This is followed by N lines, each containing two integers A_i and B_i ndicating the top-left and bottom-right corners, respectively, of the i-th rectangle.

Output

The output should contain N lines, one for each rectangle, containing the sum of the numbers contained in the correspondent rectangle.

Constraints

The following limits are guaranteed in all the test cases that will be given to your program:

1 ≤ N ≤ 1 000		Number of rectangles
1 ≤ A_i ≤ B_i ≤ 10⁹		Corners of a rectangle
1 ≤ Rows, Cols ≤ 10 000		Number of rows and columns of each rectangle
1 ≤ Sum ≤ 10¹⁸		Sum of each rectangle (the answer to each line of input)

Example Input	Example Output
4 13 51 5 31 28 44 25 245	358 160 143 7480

Explanation of the example

The four rectangles in the example correspond to the rectangles in the following figures:

the first (in red) has corners 13 and 51 and a sum of 358;
the second (in green) has corners 5 and 31 and a sum of 160;
the third (in blue) has corners 28 and 44 and a sum of 143;
the fourth (in yellow) has corners 25 and 245 and a sum of 7480.

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291

(this is an adaptation from a National Olympiad in Informatics problem)
Algorithms and Data Structures (L.EIC011) 2025/2026
DCC/FCUP & DEI/FEUP - University of Porto

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291