Aula Prática #12 - Fluxos Máximos
(semana de 14/12 a 18/12)
Exercícios para submissão
Para efeitos da nota atribuída à resolução de exercícios ao longo do semestre, os exercícios a submeter desta aula são:
Prazo de submissão: 3 de Janeiro (submeter no Mooshak de DAA)
Não se esqueçam que qualquer ajuda que tenham recebido de outros colegas deve ser reconhecida nos comentário do programa que submetem.
Depois do prazo os problemas continuarão disponíveis no Mooshak, mas as submissões não contarão para a sua nota. Relebre que cada aula vale 10% da nota desta componente.
Para um problema contar tem acertar todos os testes. Mesmo que resolva todos os problemas, o máximo numa aula é de 100%.
Conteúdos das teóricas
Nesta aula iremos abordar conceitos de Fluxos Máximos em grafos. Será por isso conveniente ver o que foi falado nas teóricas:
- Slides (capítulo "10 - Grafos: Fluxos Máximos")
- Vídeos: (vídeo #23)
Exercício 1) Introdução ao algoritmo de Edmonds-Karp
Comece por fazer download do código exemplo do algoritmo de Edmonds-Karp (que funciona em tempo \(\mathcal{O}(|V| \times |E|^2)\) [ver slides 5 a 21]:
Se costuma usar C, a sugestão é que use a última versão, que é essencialmente C com excepção do vector e queue, que já estão implementadas em C++ usando STL. A ideia é que progressivamente possa ir começando a usar as estruturas de dados úteis que o C++ tem e o C não, continuando no essencial a programar em C "normal" e usando C++ apenas para essas estruturas de dados.
- Compile e execute o código usando como input o ficheiro edmondskarp.txt, que corresponde ao grafo da figura seguinte (o mesmo que é usado na explicação de fluxo máximo nos slides):
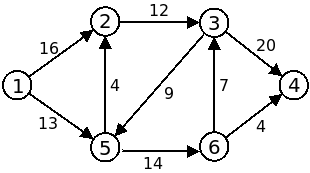
- Procure compreender todos as linhas do código dado e procure também seguir a execução, vericando se percebe os caminhos de aumento que vão sendo imprimidos, que no final dão origem a um fluxo total de 23 (12+4+7)
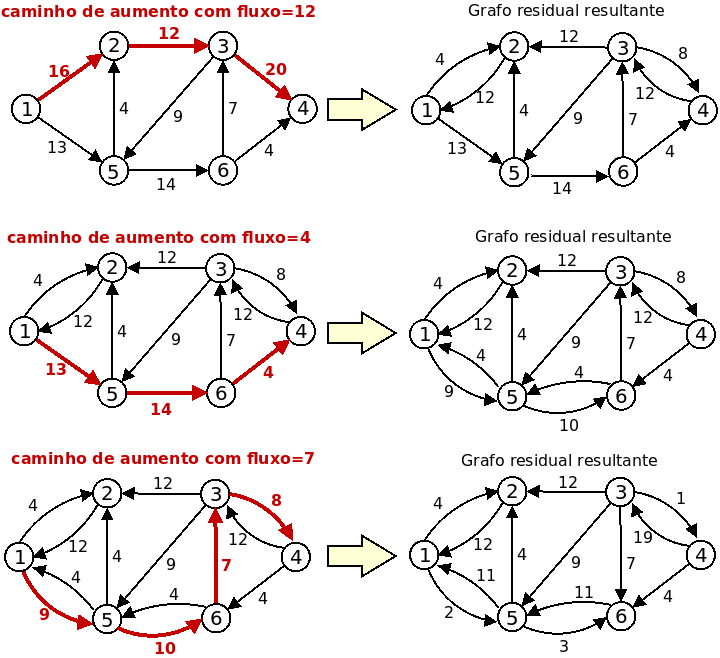
Exercício 2) Resolvendo um problema usando fluxo máximo (edge disjoint paths
Usando como base o código dado no exercício anterior, implemente e submeta uma solução para o problema [DAA 041] Corridas no parque.
Dicas:
- Para encontrar o máximo número de caminhos entre dois pontos tal que uma mesma aresta não possa aparecer em dois caminhos diferentes (edge disjoint paths) basta pensar no grafo do parque com uma rede de fluxo onde todas as arestas têm capacidade 1. Desse modo o fluxo máximo dá-nos o número máximo de caminhos que não usam as mesmas arestas (pois a sua capacidade apenas "deixa passar" um caminho) [ver slide 24].
- Tendo em conta os limites baixos no número de nós e de arestas, pode usar (quase) qualquer algoritmo, mas aqui sugerimos o Edmonds-Karp (com BFS), para o qual já tem uma implementação base. Tenha cuidado com o facto do grafo neste problema ser não dirigido (ao passo que a implementação base assume um grafo dirigido - o que tem de mudar?).
Exercício 2) Resolvendo um problema usando fluxo máximo (maximum bipartite matching
Implemente e submeta uma solução para o problema [DAA 042] Clube de livros.
Dicas:
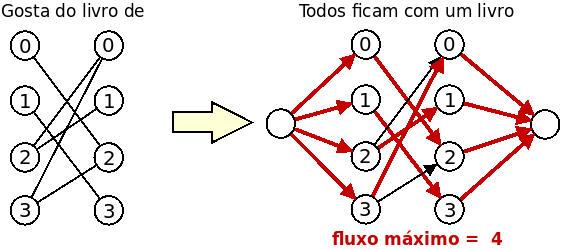
- Podemos representar as declarações de interesse por um grafo bipartido onde de um lado estão os membros do clube e do outro lado estão os livros.
- Criamos uma super-origem e um super-destino [ver slides 25 a 27]fluxo máximo.
- Se o fluxo máximo for igual ao número de membros, então temos um emparelhamento perfeito e a resposta é YES. Caso contrário a resposta é NO.
- Sugerimos usar como base a implementação dada, sendo que o problema passa quase a ser unicamente criar o grafo que representa o problema:
Material complementar
Vamos ficar pelos 42 problemas para submissão no Mooshak :) [e por isso nesta aula não existem problemas complementares]
Se quiser complementar o seu conhecimento sobre fluxos máximos com material que não foi falado na teórica (nem será alvo de avaliação no teste) pode espreitar por exemplo:
- O algoritmo de Dinic, que corre em \(\mathcal{O}(|E| \times |V|^2)\), o que é melhor que \(\mathcal{O}(|V| \times |E|^2)\) do Edmonds-Karp (ver exemplo implementação [ou português]).
- O algoritmo de Hopcraft-Karp que funciona para o caso muito específico da maximum bipartite matching, onde os pesos são 1, e por isso corre em \(\mathcal{O}(|E|\sqrt{|V|})\).
- A relação entre um corte mínimo (partição do grafo em duas partições disconexas usando arestas de peso mínimo) e o fluxo máximo: max-flow min-cut theorem
Isto serve também para relembrar que apesar de termos coberto muito material nesta unidade curricular, ainda há muitas coisas para aprenderem!
Exercício de Desafio
O exercício de desafio desta semana é um pouco diferente e com um espírito mais natalício. O objectivo é imprimir uma árvore de natal usando o menor programa possível!. A sua pontuação é igual ao tamanho do seu programa (quantidade de bytes): quanto menor melhor!
O prémio para as 5 melhores soluções no final do dia 3 de Janeiro (1 dia antes do exame) é um lanche no Alicantina pago por mim, Pedro Ribeiro (mais companhia para pequena conversa sobre algoritmos - possivelmente não todos ao mesmo tempo por causa do distanciamento)
Este desafio está disponível para submissão no Mooshak (têm de usar C, C++ ou Java):
[DAA XMAS] Árvore de Natal
Bom Natal e Feliz Ano Novo para todos!