Para efeitos da nota atribuída à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 15 de Novembro
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #05]
[DAA 017] Pirâmides
(este problema é essencialmente o mesmo que criei para uma fase de seleção das ONI)
 As pirâmides do Egipto são
túmulos. Os faraós que as mandaram construir e os arquitectos que as
desenharam, não as prepararam para que os turistas do século XXI se
divertissem subindo-as. No entanto, há sempre alguns visitantes mais
ousados que ultrapassam as barreiras de segurança e se aventuram a
trepar as pirâmides, para chegar lá acima e acenar estupidamente a
bandeira do seu país.
As pirâmides do Egipto são
túmulos. Os faraós que as mandaram construir e os arquitectos que as
desenharam, não as prepararam para que os turistas do século XXI se
divertissem subindo-as. No entanto, há sempre alguns visitantes mais
ousados que ultrapassam as barreiras de segurança e se aventuram a
trepar as pirâmides, para chegar lá acima e acenar estupidamente a
bandeira do seu país.
Trepar as pirâmides é difícil e perigoso. Cada pirâmide é formada por
camadas de pedras. Admitamos que a camada inferior, tem, em cada face,
N pedras. A segunda camada, em cima dessa, terá N-1 pedras, cada uma
apoiada sobre duas pedras inferiores. Assim, haverá N camadas. Para
trepar a pirâmide, cada um destes "alpinistas" de algibeira, começa
por subir uma das pedras da base; depois, passa dessa para uma das
duas pedras da segunda camada que se apoiam sobre a pedra que ele
trepou inicialmente; e assim sucessivamente, até chegar ao topo. Se a
pirâmide estivesse em bom estado, com todas as pedras no lugar, haveria
2N-1 "maneiras" diferentes de subir até ao topo, cada maneira
correspondendo a um percurso pela pirâmide acima. No entanto, as
pirâmides estão bastante degradadas e algumas pedras faltam ou estão
tão deterioradas que se torna impossível subir para cima delas, para
daí continuar a escalada. Fica assim a questão: nestas condições,
quantas maneiras diferentes haverá de trepar a pirâmide até ao topo?
O Problema
Escreva um programa que dada uma pirâmide com N camadas, e uma
descrição das pedras em falta ou muito deterioradas numa das faces da
pirâmide, calcule o número de maneiras diferentes de subir a pirâmide
até ao topo, começando por uma qualquer das pedras da primeira camada,
evitando as pedras que estão em falta ou muito deterioradas.
Input
Na primeira linha vem o número N que
representa o número de pedras na primeira camada e também o número de
níveis da pirâmide. Na segunda linha vem o número
D de pedras em falta ou muito deterioradas. Nas D linhas seguintes vêm dois números, Ci e Pi, que
descrevem cada uma destas pedras em falta ou muito deterioradas: C
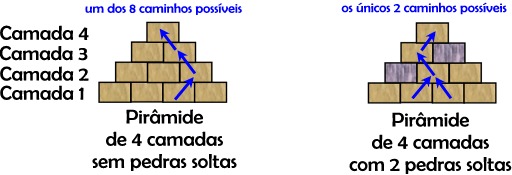
representa a camada (como indicado na figura), e Pi representa a posição da pedra nessa camada (onde 1 é a pedra mais à esquerda, 2 a 2ª pedra mais esquerda, etc).
Output
Uma única linha com indicando M, o número de
maneiras diferente de subir a pirâmide.
Restrições
São garantidos os seguintes limites em todos os casos de teste
que irão ser colocados ao programa:
| 1 ≤ N ≤ 1000 |
|
Quantidade de níveis da pirâmide |
| 0 ≤ D ≤ N * (N + 1) / 2 |
|
Quantidade de pedras em falta ou deterioradas |
| 1 ≤ Ci ≤ N |
|
Camada da i-ésima peda em falta ou deteriorada |
| 1 ≤ Pi ≤ N-(C-1) |
|
Posição da i-ésima peda em falta ou deteriorada |
| 0 ≤ M < 263 |
|
Número de maneiras diferentes de subir a pirâmide |
Exemplo de Input 1
4
2
2 1
3 2
Exemplo de Output 1
2
Explicação do Input/Output 1
Este input à imagem do lado direito da figura do enunciado: uma pirâmide com 4 camadas e 2 pedras estragadas:
- a 1ª pedra da camada 2 (linha de input "2 1")
- a 2ª pedra da camada 3 (linha de input "3 2")
Exemplo de Input 2
5
3
3 2
2 3
1 4
Exemplo de Output 2
5
Desenho e Análise de Algoritmos (CC2001)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto
 As pirâmides do Egipto são
túmulos. Os faraós que as mandaram construir e os arquitectos que as
desenharam, não as prepararam para que os turistas do século XXI se
divertissem subindo-as. No entanto, há sempre alguns visitantes mais
ousados que ultrapassam as barreiras de segurança e se aventuram a
trepar as pirâmides, para chegar lá acima e acenar estupidamente a
bandeira do seu país.
As pirâmides do Egipto são
túmulos. Os faraós que as mandaram construir e os arquitectos que as
desenharam, não as prepararam para que os turistas do século XXI se
divertissem subindo-as. No entanto, há sempre alguns visitantes mais
ousados que ultrapassam as barreiras de segurança e se aventuram a
trepar as pirâmides, para chegar lá acima e acenar estupidamente a
bandeira do seu país.