Para efeitos da nota atribuida à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 12 de Junho
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #12]

[DAA 041] Corridas no parque

O Aniceto adora correr no parque da cidade. Todos os dias ele faz o seu treino e não conseguiu deixar de reparar que por vezes era aborrecido percorrer caminhos iguais. Decidido a quebrar a monotonia, ele decidiu encontrar o maior número possível de caminhos que nunca repetem o mesmo trilho.

O parque pode ser pensado como um grafo com V nós e E arestas, onde cada aresta é um trilho a ligar dois nós (pode correr-se em qualquer um dos sentidos). Um exemplo é o parque da seguinte figura, com 14 nós e 24 trilhos:

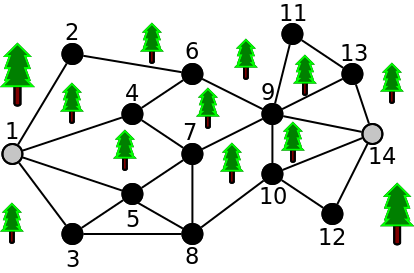
O Aniceto quer sempre correr entre o primeiro nó (indicado pelo número 1) e o último nó (identificado pelo número V - no caso da figura o nó 14). Dois caminhos dizem-se diferentes se nunca repetirem uma mesma aresta, ou seja, se seguirem sempre por trilhos diferentes (mesmo que passem por nós iguais). Para o exemplo de figura anterior, existem no máximo 3 caminhos diferentes que nunca repetem trilhos (indicados a azul, verde e vermelho):

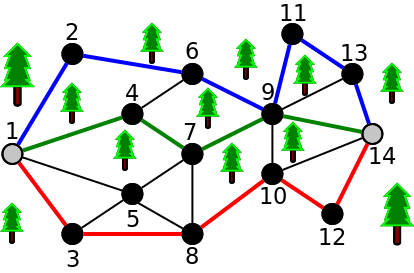
Nota que existem outros caminhos possíveis, mas nunca se consegue criar mais do que 3 caminhos diferentes que não partilhem pelo menos um trilho. Uma outra maneira de obter os 3 caminhos seria:

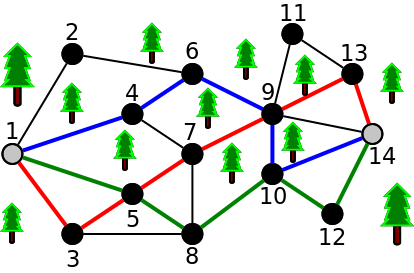
O Problema

Dado o mapa do parque (o grafo), tens de ajudar o Aniceto a descobrir qual o maior número de caminhos diferentes (sem partilhar arestas) que se consegue formar entre o primeiro e o último nó.

Input

A primeira linha contém dois inteiros V e E indicando respectivamente o número de nós e de arestas (trilhos) a considerar.

Seguem-se exactamente E linhas, cada uma com dois inteiros A B, indicando que existe um trilho (bidirecional) entre os nós A e B.

Os nós são representados por inteiros entre 1 e V (inclusive) e é garantido que existe sempre pelo menos um caminho entre 1 e V.

Output

O output deve ser constituído por uma única linha indicando o número máximo de caminhos diferentes (sem partilhar trilhos) que podem existir entre o nó 1 e o nó V.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

Exemplo de Input

14 24
1 2
1 4
1 5
1 3
2 6
4 6
4 7
3 5
3 8
5 7
5 8
7 8
7 9
6 9
8 10
10 9
11 9
13 11
13 9
14 9
10 14
10 12
12 14
14 13

Exemplo de Output

3

Explicação do Input/Output

O exemplo de input corresponde à figura do enunciado.

Desenho e Análise de Algoritmos (CC2001)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto