Para efeitos da nota atribuída à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 12 de abril
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #04]

[DAA 016] Invasão espacial
(este problema é essencialmente o mesmo que criei para uma MIUP)

És o responsável pela defesa de Algo, a capital do planeta MIUP. A cidade pode ser pensada como um longo segmento 1D com um conjunto de N edíficios muito altos e estreitos, alojando toda a administração planetária. Cada edifício pode ser identificado por três inteiros: a sua posição Xi, a sua altura Yi e a força do seu gerador de escudo Pi (nota que todos os edifícios têm largura de uma unidade).

Sabes que as forças malévolas do planeta Complexidade estão a planear atacar a tua cidade e precisas de te preparar. O inimigo vai atacar com naves espaciais vindas do céu que podem disparar lasers diretamente de cima para baixo, atingindo a cidade.

Podes construir escudos horizontais, que podem ser instalados no topo de qualquer edifício. Um edifício i com um escudo irá proteger-se a si próprio e também irá proteger todos os edifícios j que não são mais altos (Yi ≤ Yj), que estão no máximo a Pi distância (|Xi - Xj| ≤ Pi) e que não têm edifícios mais altos entre eles (isto é, para todo o k entre i e j, Yi ≥ Yk).

Os escudos são no entanto muito caros. Queres por isso construir o menor número possível de escudos, de modo a poupar dinheiro, de tal modo que todos os edíficios estejam protegidos por pelo menos um escudo.

O Problema

Dadas as posições, alturas e forças dos gerados de escudos de cada um dos edifícios da tua cidade, a tua tarefa é calcular o menor de escudos que precisam de ser instalados de tal modo que todos os edifícios estão protegidos dos ataques das naves espaciais inimigas.

Input

A primeira linha contém um inteiro N, o número de edifícios. Seguem-se N linhas, cada uma contendo a descrição de um dos edifícios da cidade. Cada uma destas linhas contém três inteiros Xi Yi Pi, respetivamente a posição horizontal, a altura e a força do gerador de escudo. Os edifícios podem vir por qualquer ordem e nunca existem dois edifícios com a mesma posição horizontal.

Output

Uma linha com um único inteiro indicando o menor número possível de escudos a usar de modo a que todos os edíficos fiquem protegidos.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

1 ≤ N ≤ 100 000     Quantidade de edifícios
0 ≤ Xi ≤ 109     Posição horizontal de um edifício
0 ≤ Hi ≤ 109     Altura de um edifício
0 ≤ Pi ≤ 109     Poder do gerador de escudo de um edifício

Exemplo de Input 1

8
8 5 20
4 6 0
10 7 1
19 4 1
13 9 3
14 12 2
16 10 2
12 8 4

Exemplo de Output 1

4

Explicação do Input/Output 1

Uma possível escolha de 4 escudos seria:

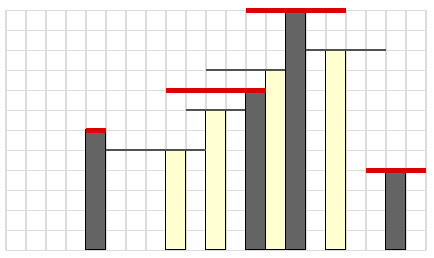
Exemplo de Input 2

14
3 4 3
5 4 2
7 4 3
11 10 2
12 9 2
13 8 2
14 7 1
21 11 4
20 10 3
19 9 2
18 6 2
15 1 0
16 2 0
17 3 0

Exemplo de Output 2

5

Explicação do Input/Output 2

Uma possível escolha de 5 escudos seria:

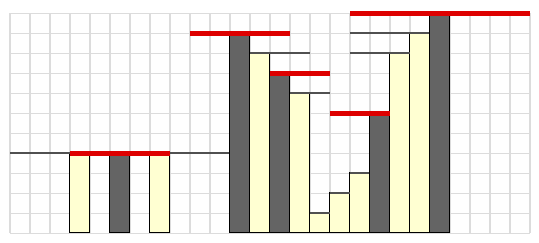
Nas figuras das explicações, as linhas pretas "finas" indicam os possíveis escudos, e as linhas vermelhas "grossas" indicam os escudos selecionados. Além disso, os edíficios a amarelo claro são os protegidos por escudos de outros, enquanto que os edífícios a cinzento escuro são os que têm escudos construídos no seu topo.

Desenho e Análise de Algoritmos (CC2001)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto