Para efeitos da nota atribuída à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 3 de maio
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #06]

[DAA 022] Árvores red-black

As árvores red-black são um tipo de árvores binárias de pesquisa "equilibradas" que garantem tempo logarítmico nas operações típicas de pesquisa, inserção e remoção de elementos.

Para que uma árvore binária de nós pretos e vermelhos seja considerada red-black tem que obedecer a várias restrições. Antes de tudo o resto, tem de ser uma árvore binária de pesquisa, ou seja, para qualquer nó da árvore, todos os nós descendentes à sua esquerda têm de ser menores, e todos os nós descendentes à sua direita têm de ser maiores. Para além disso, tem de respeitar as seguintes propriedades:

• (root property) A raíz da árvore é preta
• (leaf property) As folhas são nós (nulos/vazios) pretos
• (red property) Os filhos de um nó vermelho são pretos
• (black property) Para cada da nó, um caminho para qualquer uma das suas folhas descendentes tem o mesmo número de nós pretos

O Problema

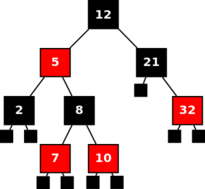
Dada uma árvore binária constituída unicamente por nós pretos e vermelhos, a tua tarefa é determinar se ela é uma árvore red-black, ou seja, se é árvore binária de pesquisa e se obedece às propriedades descritas.

Input

Na primeira linha do input está um número A indicando a quantidade de árvores a considerar.

Seguem-se A linhas, cada uma com N_i inteiros entre -1000 e 1000 descrevendo descrevendo uma árvore red-black em preorder (raíz, sub-árvore esquerda, sub-árvore direita). Um número positivo indica um nó preto com esse valor. Um número negativo indica um nó vermelho contendo o valor absoluto do número (ex: -5 indica um nó vermelho contendo o número 5). O número zero representa uma folha nula preta.

A título de exemplo, a árvore da figura de cima é descrita por:

12 -5 2 0 0 8 -7 0 0 -10 0 0 21 0 -32 0 0

É garantido que não existem números repetidos na árvore.

Output

O output deve ter exactamente A linhas. Em cada uma delas deve ser imprimido SIM ou NAO consoante a árvore respectiva seja ou não uma red-black tree.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

Exemplo de Input

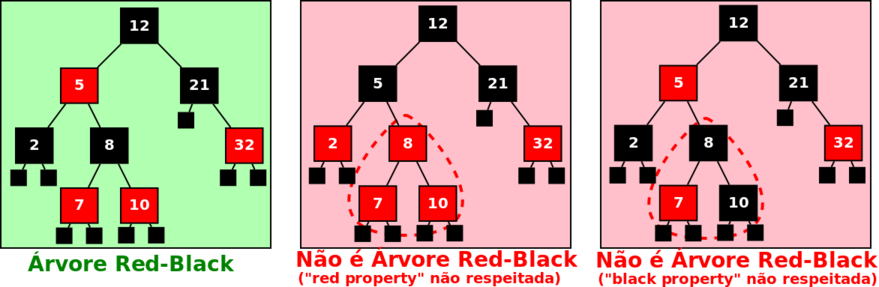
3
12 -5 2 0 0 8 -7 0 0 -10 0 0 21 0 -32 0 0
12 5 -2 0 0 -8 -7 0 0 -10 0 0 21 0 -32 0 0
12 -5 2 0 0 8 -7 0 0 10 0 0 21 0 -32 0 0

Exemplo de Output

SIM
NAO
NAO

Explicação do Input/Output

O exemplo de input corresponde às seguintes 3 árvores:

Desenho e Análise de Algoritmos (CC2001)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto