Para efeitos da nota atribuida à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 17 24 de maio
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #08]
Tens de ajudar um grupo de biólogos a analisarem uma rede de interação de proteínas. Os biológos resolveram modelar a rede como um grafo não dirigido e não pesado e estão interessados em dados sobre distâncias entre nós. Podes assumir que a rede que estão a estudar é completamente conexa, ou seja, existe um caminho entre qualquer par de nós do grafo associado.
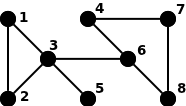
Considera por exemplo a rede modelada pelo grafo da seguinte figura:

A distância mínima entre dois nós do grafo é o número mínimo de arestas num caminho entre esses dois nós. Para a rede da figura, uma matriz de distâncas mínimas seria:
| Nos | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | -- | 1 | 1 | 3 | 2 | 2 | 4 | 3 |
| 2 | 1 | -- | 1 | 3 | 2 | 2 | 4 | 3 |
| 3 | 1 | 1 | -- | 2 | 1 | 1 | 3 | 2 |
| 4 | 3 | 3 | 2 | -- | 3 | 1 | 1 | 2 |
| 5 | 2 | 2 | 1 | 3 | -- | 2 | 4 | 3 |
| 6 | 2 | 2 | 1 | 1 | 2 | -- | 2 | 1 |
| 7 | 4 | 4 | 3 | 1 | 4 | 2 | -- | 1 |
| 8 | 3 | 3 | 2 | 2 | 3 | 1 | 1 | -- |
A excentricidade de um nó é igual à maior distância mínima dele próprio a um qualquer outro nó. Por exemplo:
excentricidade(1) = 4 excentricidade(3) = 3
Os biólogos estão a tentar perceber a importância dos vários nós e por isso querem saber várias coisas sobre a excentricidade. Em particular, desejam saber as seguintes propriedades da rede:
Tens de ajudar os biólogos a conseguirem estes dados.
Dada um grafo conexo não dirigido e não pesado descrevendo uma rede biológica, a tua tarefa é calcular o seu diâmetro, o seu raio, quais os nós centrais e quais os nós periféricos.
Na primeira linha vem um único número inteiro N indicando o número de nós do grafo a considerar. Os nós são identificados por números inteiros consecutivos de 1 até N.
Na segunda linha vem um único número inteiro E indicando o número de arestas do grafo. Seguem-se E linhas, cada uma contendo dois inteiros A e B indicando que existe uma aresta (ligação direta) entre os nós A e B.
As arestas podem vir por qualquer ordem mas é garantido que nunca aparecem arestas repetidas. É também garantido que dão origem a um grafo completamente conexo.
O exemplo de input corresponde à figura dada anteriormente.
Na primeira linha deve vir um único inteiro indicando o diâmetro da rede.
Na segunda linha deve vir um único inteiro indicando o raio.
Na terceira linha devem vir os nós centrais. Se existir mais que um nó central, deves escrevê-los por ordem crescente e com um espaço a separar cada par de nós.
Na quarta linha devem vir os nós periféricos. Se existir mais que um nó periférico, deves escrevê-los por ordem crescente e com um espaço a separar cada par de nós.
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| 1 ≤ N ≤ 1500 | Número de nós | |
| 1 ≤ E ≤ 5000 | Número de arestas (ligações) |
8 9 1 3 2 3 3 5 3 6 6 4 6 8 4 7 1 2 8 7
4 2 6 1 2 5 7
O exemplo de input corresponde à figura do enunciado.
Desenho e Análise de Algoritmos (CC2001)
DCC/FCUP - Faculdade de Ciências da Universidade do Porto