Para efeitos da nota atribuida à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 8 de Janeiro
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #09]
[ED199] Tesouros de Kilmia
Neste problema deverá submeter uma classe ED199 contendo um programa completo para resolver o problema (ou seja, com o método main).
 Depois de
muitos anos como concorrente de concursos de programação, muitas
edições de qualificações, finais e outras provas das ONI, o Daniel
decidiu finalmente reformar-se. Como próximo desafio, o Daniel
escolheu fazer algo que seja igualmente emocionante. Decidiu por isso
tornar-se caçador de tesouros!
Depois de
muitos anos como concorrente de concursos de programação, muitas
edições de qualificações, finais e outras provas das ONI, o Daniel
decidiu finalmente reformar-se. Como próximo desafio, o Daniel
escolheu fazer algo que seja igualmente emocionante. Decidiu por isso
tornar-se caçador de tesouros!
O seu próximo alvo está em Kilmia, uma aldeia localizada numa
pequena ilha próxima da Península Arábica. Aqui se encontra a
grande linha de Algor, uma linha com N arcas enterradas
lado a lado. Algumas destas arcas contêm tesouros de enorme
valor, que naturalmente o Daniel quer recolher.
Para recolher o máximo de tesouros, inicialmente o Daniel
coloca-se em cima da B-ésima arca. Depois, ele segue um
conjunto de I instruções escritas num velho mapa da
região, de forma a percorrer as várias arcas. Cada instrução é
da forma "anda X passos para a direita" ou "anda X passos para a
esquerda". Um passo para a direita corresponde a avançar para a
próxima arca no sentido este, um passo para a esquerda
corresponde a avançar para a próxima arca no sentido
oeste. Adicionalmente, sempre que o Daniel passa por uma arca
(mesmo que esteja a meio de cumprir uma instrução), ele
desenterra-a e recolhe o tesouro no seu interior, caso haja.
Nota que o Daniel desenterra sempre a arca na posição onde começa,
B.
Por exemplo, vamos considerar que há N = 5 arcas, sendo
que todas as arcas tirando a segunda têm tesouro, e que o Daniel
inicialmente se encontra na posição B = 3. A seguinte
imagem representa esta situação:
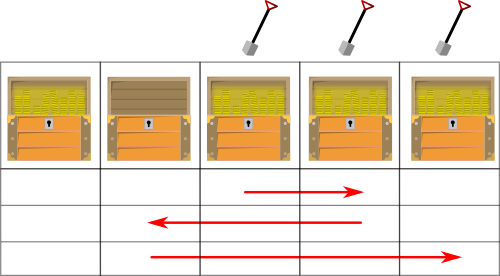
No mapa do Daniel são dadas as seguintes I = 3 instruções:
Anda 1 passo para a direita
Anda 2 passos para a esquerda
Anda 3 passos para a direita
As setas na imagem representam estes movimentos. O Daniel passa
por várias arcas e no fim pode recolher exatamente 3 tesouros
(marcados na imagem com pás).
O Daniel terminou a sua aventura, mas ele precisa de saber
quantos tesouros conseguiu recolher... mas são tantos! Ajuda-o a contar
quantos tesouros recolheu, tendo em conta a sua posição inicial e
as instruções que ele seguiu.
O Problema
Dado um conjunto de N arcas da linha de Algor, a posição
inicial do Daniel B e um conjunto de instruções sobre o
movimento do Daniel, calcula quantos tesouros o Daniel recolhe.
Input
Na primeira linha vêm três inteiros, N que representa o
número de arcas, B que representa a posição inicial do
Daniel e I que representa o número de instruções.
Segue-se uma linha com N caracteres que podem ser 'T' ou
'V' ('T'esouro, 'V'azia), sendo que o i-ésimo carácter
representa o tipo da i-ésima arca, 'T' para uma arca com tesouro
e 'V' para uma arca sem tesouro.
Seguem-se I linhas, cada uma com o seguinte
formato: D P, onde D é um carácter que pode
ser 'D' ou 'E' ('D'ireita, 'E'squerda), representado o sentido
do movimento, e P é um inteiro que representa o número de
passos a dar.
Nota: é garantido que as instruções nunca obrigam o
Daniel a sair fora da linha de arcas, ou seja, a sua posição
será sempre entre 1 e N.
Output
O output contém um inteiro, o número de tesouros recolhidos pelo
Daniel.
Restrições
São garantidos os seguintes limites em todos os casos de teste que
irão ser colocados ao programa:
| 1 ≤ N ≤ 100 000 |
|
Número de arcas |
| 1 ≤ B ≤ N |
|
Posição inicial |
1 ≤ I ≤ 100 000 |
|
Número de instruções |
Os casos de teste deste problema estão organizados em 4 grupos
com restrições adicionais diferentes:
| Grupo |
Número de Pontos |
Restrições adicionais |
| 1 |
25 |
1 ≤ N ≤ 100, 1 ≤ I ≤ 100 |
| 2 |
20 |
1 ≤ I ≤ 3 000 |
| 3 |
20 |
1 ≤ N ≤ 3 000 |
| 4 |
35 |
- |
Input do Exemplo 1
5 3 3
TVTTT
D 1
E 2
D 3
Output do Exemplo 1
3
Explicação do Exemplo 1
Este exemplo corresponde ao mencionado no enunciado.
Input do Exemplo 2
10 5 9
TTTTVTTTTT
D 1
E 2
D 1
D 1
D 1
E 3
E 1
D 4
D 1
Output do Exemplo 2
5
(adaptação para a UC de Estruturas de Dados - CC1007 - DCC/FCUP)
Qualificação para a final das ONI'2017
(30/03 a 01/04 de 2017)
 Depois de
muitos anos como concorrente de concursos de programação, muitas
edições de qualificações, finais e outras provas das ONI, o Daniel
decidiu finalmente reformar-se. Como próximo desafio, o Daniel
escolheu fazer algo que seja igualmente emocionante. Decidiu por isso
tornar-se caçador de tesouros!
Depois de
muitos anos como concorrente de concursos de programação, muitas
edições de qualificações, finais e outras provas das ONI, o Daniel
decidiu finalmente reformar-se. Como próximo desafio, o Daniel
escolheu fazer algo que seja igualmente emocionante. Decidiu por isso
tornar-se caçador de tesouros!
