Para efeitos da nota atribuida à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 29 de Outubro
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #04]

[ED246] Caderno Quadriculado

A Sara adora o seu caderno quadriculado de matemática. Para passar o tempo começou a escrever os números inteiros consecutivamente. Achou, contudo, que fazê-lo de esquerda para a direita e de cima para baixo era muito aborrecido! Resolveu por isso preencher os números pelas diagonais usando o seguinte padrão:

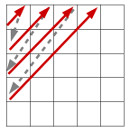
Isto resulta num preenchimento das quadrículas como representado a seguir, onde se vê parte do caderno da Sara (as outras linhas e colunas que não aparecem na figura estão preenchidas com números também):

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

A Sara acha que ficou um padrão muito giro! Como na sua escola está na fase de aprender a operação de adição, resolveu começar a somar os números contidos dentro de retângulos. Por exemplo, se considerasse o retângulo da figura seguinte (com cantos nos números 13 e 51), a soma seria igual a 358 (13+19+26+34+18+25+33+42+24+32+41+51):

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

A Sara gostava de poder verificar se as somas estão corretas. Claro que ela gostava de saber a soma de um qualquer retângulo dado. Será que podes ajudá-la?

O Problema

Dado um conjunto de N retângulos, cada um indicado pelos números nos seus cantos A_i e B_i, determina a soma dos números contidos em cada retângulo, supondo que o caderno quadriculado foi preenchido pelas diagonais como atrás descrito. Podes assumir que o caderno tem um tamanho tão grande que a Sara tem sempre uma quadrícula disponível quando precisa de escrever um novo número.

Input

Na primeira linha vem um inteiro N, indicando o número de retângulos a considerar. Seguem-se N linhas, cada uma com dois inteiros A_i e B_i indicando os cantos superior esquerdo e inferior direito, respectivamente, do i-ésimo retângulo.

Output

O output deve contar N linhas, uma para cada retângulo, contendo a soma do dos números nele contidos.

Restrições

São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:

1 ≤ N ≤ 1 000		Número de retângulos
1 ≤ A_i ≤ B_i ≤ 10⁹		Cantos de cada retângulo
1 ≤ Linhas, Colunas ≤ 10 000		Número de linhas e colunas de cada retângulo
1 ≤ Resposta ≤ 10¹⁸		Soma de cada retângulo (a resposta)

Os casos de teste deste problema estão organizados em 3 grupos com restrições adicionais diferentes:

Grupo	Número de Pontos	Restrições adicionais
1	40	1 ≤ A_i ≤ B_i ≤ 500
2	30	Os retângulos não têm mais do que 50 linhas e 50 colunas
3	30	-

Input do Exemplo

Output do Exemplo

Explicação do Exemplo

Os quatro retângulos do exemplo correspondem aos retângulos das figuras seguintes:

o primeiro (a vermelho) tem cantos 13 e 51 e uma soma de 358;
o segundo (a verde) tem cantos 5 e 31 e uma soma de 160;
o terceiro (a azul) tem cantos 28 e 44 e uma soma de 143;
o quarto (a amarelo) tem cantos 25 e 245 e uma soma de 7480.

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291

(adaptação para a UC de Estruturas de Dados - CC1007 - DCC/FCUP)

Qualificação para a final das ONI'2016
(07/04 a 09/04 de 2016)

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36
2	5	9	14	20	27	35	44
4	8	13	19	26	34	43	53
7	12	18	25	33	42	52	63
11	17	24	32	41	51	62	74
16	23	31	40	50	61	73	86

1	3	6	10	15	21	28	36	45	55	66	78	91	105	120
2	5	9	14	20	27	35	44	54	65	77	90	104	119	135
4	8	13	19	26	34	43	53	64	76	89	103	118	134	151
7	12	18	25	33	42	52	63	75	88	102	117	133	150	168
11	17	24	32	41	51	62	74	87	101	116	132	149	167	186
16	23	31	40	50	61	73	86	100	115	131	148	166	185	205
22	30	39	49	60	72	85	99	114	130	147	165	184	204	225
29	38	48	59	71	84	98	113	129	146	164	183	203	224	246
37	47	58	70	83	97	112	128	145	163	182	202	223	245	268
46	57	69	82	96	111	127	144	162	181	201	222	244	267	291