Para efeitos da nota atribuida à resolução de exercícios ao longo do semestre - Submeter até 23:59 de 3 de Dezembro
(o problema continuará depois disponível para submissão, mas sem contar para a nota)
[para perceber o contexto do problema deve ler o guião da aula #08]

Orientação é um desporto em que o objectivo é percorrer uma determinada distância em terreno variado e desconhecido, obrigando os atletas a passar por N pontos no terreno (chamados postos de controlo), descritos num mapa distribuído a cada atleta no início da prova.
A Sociedade Atlética de Trás-os-Montes (SAT) realiza, todos os anos, a Orientação Nacional Impossível (ONI), a prova mais importante e difícil de orientação a nível nacional. Para além de terem que passar pelos N postos de controlo, estes têm que ser percorridos por uma certa ordem. Porém, a prova é muito dura e por isso a maior parte não a termina, conseguindo apenas percorrer alguns dos primeiros postos de controlo.
Este ano houve M participantes na ONI, sendo que o i-ésimo participante chegou até ao posto de controlo Di, ou seja, passou pelos primeiros Di postos de controlo até terminar a sua prova.
Considerem que há N=8 postos de controlo e que houve M=3 participantes na corrida deste ano, que chegaram até aos postos de controlo de 2, 6 e 4, respetivamente. A imagem seguinte representa esta situação:
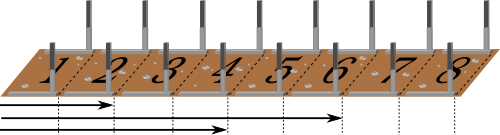
Este ano, a SAT decidiu ir mais longe e instalar câmaras em cada posto de controlo, permitindo aos aficionados reverem a prova, do conforto de suas casas. Por uma módica quantia, os fãs terão acesso às imagens de uma das câmaras. De forma a permitir aos fãs uma escolha informada da câmara que pretendem observar, a organização disponibilizou no seu site uma ferramenta de pesquisa que responde, para um dado posto de controlo, quantos atletas picaram o ponto nesse posto de controlo.
Para o exemplo acima temos que 3 atletas passaram o primeiro e segundo postos, 2 passaram o terceiro e quarto postos, um o quinto e sexto e nenhum passou os restantes. A imagem seguinte contém esta informação ao pé de cada câmera.
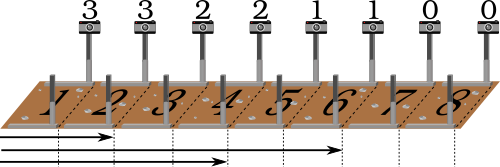
A tua tarefa é implementar esta ferramenta, ou seja, dados os postos de controlo em que cada atleta terminou Di a sua prova é suposto responder a uma sequência de Q perguntas, onde a i-ésima pergunta requer quantos atletas passaram pela câmera no posto qi.
Dados N postos de controlo, M participantes na ONI, bem como os postos de controlo Di em que cada atleta terminou a sua prova, e Q perguntas qi sobre câmeras, descobrir quantos participantes passaram por cada uma das câmeras dadas.
Na primeira linha linha vêm dois inteiros, N, que representa o número de postos de controlo, e M, o número de participantes.
Segue-se uma linha com M inteiros, onde o i-ésimo representa Di, o postos de controlo em que o atleta i finalizou a prova.
Segue-se uma linha um inteiro Q, o número de perguntas a fazer.
Finalmente, segue-se uma linha com Q inteiros qi, para os quais queremos saber quantos participantes chegaram à câmera no posto de controlo qi.
Q linhas, uma por cada pergunta, com apenas um número, representando o número de participantes que passaram pela câmera do posto de controlo qi.
São garantidos os seguintes limites em todos os casos de teste que irão ser colocados ao programa:
| 1 ≤ N ≤ 1 000 000 000 | Número de postos de controlo | |
| 1 ≤ M ≤ 100 000 | Número de participantes | |
| 1 ≤ Di ≤ N | Postos de controlo finais de cada atleta | |
| 1 ≤ Q ≤ 50 000 | Número de perguntas sobre postos de controlo | |
| 1 ≤ qi ≤ N | Números de câmeras |
Os casos de teste deste problema estão organizados em 4 grupos com restrições adicionais diferentes:
| Grupo | Número de Pontos | Restrições adicionais |
|---|---|---|
| 1 | 20 | 1 ≤ N ≤ 1 000, 1 ≤ Q ≤ 1 000, 1 ≤ M ≤ 10 000 |
| 2 | 25 | 1 ≤ Q ≤ 1 000, 1 ≤ M ≤ 10 000 |
| 3 | 25 | 1 ≤ N ≤ 100 000 |
| 4 | 30 |
8 3 2 6 4 8 1 2 3 4 5 6 7 8
3 3 2 2 1 1 0 0
Este exemplo corresponde ao mencionado no enunciado.
100 5 1 10 100 1 10 3 10 1 100
3 5 1