
In what concerns the "exercises during classes" component of the evaluation, the exercises that you can submit for this class are:
Deadline for submission: December 14th (submit to IP's Mooshak)
You are encouraged to talk to the professors and your colleagues if you encounter difficulties.
However, any more direct help that you receive should be acknowledged in the comments of the code you submit.
After the deadline the problems will still be available on Mooshak, but the submissions will not count towards your grade.
Each practical class is worth 10% of your final component for exercices during class. Since there will be 11 classes with submissions, you can achieve maximum grade even without doing all classes.
For a problem to count you must pass all tests (that is, to have an accepted). Even if you solve all problems, the maximum on one class is 100%.
To obtain 100% it will always be enough to solve the main exercises.
With the exercises in this class you will develop the following skills:
This week's exercises are a bit more complex and algorithmically rich: they are more about programming in itself and less just about Python.
You should first try to read and understand the respective lecture: T15 and T16: Recursion
This week's theme for the exercises is Futurama.

1) Recursion examples
Make sure you understand the following recursive definitions of list summation given in the lecture, demonstrating two very common patterns:
# A first recursive definition of mysum # Notice the use of slicing to extract everything but the 1st element def mysum_v3(lst): # print(f"mysum_v3({lst})") # uncomment to see the calls if len(lst) == 1: return lst[0] # base case return lst[0] + mysum_v3(lst[1:]) # recursive case print(mysum_v3([1,2,3,4]))
Here is the recursive tree showing the calls being made in this first recursive function:
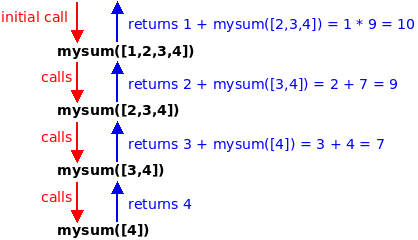
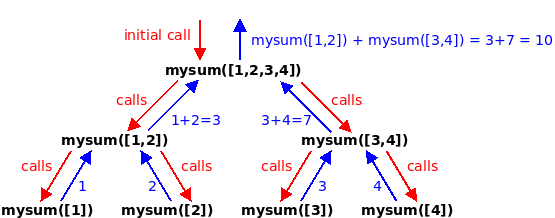
# Recursive definition of mysum splitting into two halfs def mysum_v5(lst): # print(f"mysum_v5({lst})") # uncomment to see the calls if len(lst) == 1: return lst[0] # base case middle = len(lst) // 2 # integer division return mysum_v5(lst[:middle]) + mysum_v5(lst[middle:]) # recursive case print(mysum_v5([1,2,3,4]))
Here is the recursive tree showing the calls being made in this second recursive function:
2) My first recursion
Implement a recursive method palindrome(word) that given a string word constituted by lower case letters, returns True if the word is a palindrome and False if it isn't.
How can you divide the problem into simpler tasks and into one or more smaller instances of the same problem?
Test your method in your computer (and after testing you can even try to submit to [IP037] which was available on class #05 (of course on that time you did it differently, right?)
- Compare the first letter with the last:if they are different, you can return false
- If they are the same, continue with the rest of the word (everything except the first and last character
- Stop when the problem is simple enough (what is the base case here?)
3) A recursive mooshak problem [main]
![]()
For this exercise you will be solving the problem [IP085] Dataset Confusion.
Read the statement, code and try to submit an Accepted solution. Don't forget to test first on your computer!
For this problem you should first see the flatten example code that was given in the lecture. Read it carefully and understand how it works:
# recursive function def flatten(lst): if not isinstance(lst, list): return [lst] # base case 1: not a list if len(lst) == 0: return [] # base case 2: empty list return flatten(lst[0]) + flatten(lst[1:]) # recursive cals print(flatten([[[[4,1],7]],3,[[2]],[5,6],[[42],[40]],[[[[[[[10]]]]]]]]))
After understanding, you are ready to adapt/extend it to the problem at hand!
- How to use isinstance to detect if it is an int? When you detect it, just return its value
- Tuples, like lists, are sequences, so we can use indexing and splicing
- You can still use + to combine, but instead of concatenating you will be... summing
- The base case now should not return []... but zero, which is the neutral element of the sum operation
4) Generating strings [main]
![]()
For this exercise you will be solving the problem [IP086] Binary Communication.
Read the statement, code and try to submit an Accepted solution. Don't forget to test first on your computer!
For this problem you should first see the AB strings generation example code that was given in the lecture. Read it carefully and understand how it works (the lecture includes a recursive tree):
# recursive function # k: remaining size to generate # cur: current string being built def gen_v2_rec(k, cur): if k == 0: return [cur] # base case l1 = gen_v2_rec(k-1, cur + "A") # recursive case 1 l2 = gen_v2_rec(k-1, cur + "B") # recursive case 2 return l1 + l2 # combine both results # main function that calls auxiliary recursive function def gen_v2(k): return gen_v2_rec(k, "") print(gen_v2(3)) # all strings of size 3 with As and Bs
After understanding, you are ready to adapt/extend it to the problem at hand!
- Instead of As and Bs... you will have 0s and 1s
- On the lecture it also shown how to limit the number of a certain character (e.g. using an extra parameter to indicate the amount left)
- How to generate more than one size? You can either do it separately and then concatenate or just generate all at once by always adding to the result when you are within the desired size range
5) Generating sequences of planets [main]
![]()
For this exercise you will be solving the problem [IP087] Planetary Weekends.
Read the statement, code and try to submit an Accepted solution. Don't forget to test first on your computer!
This is almost like the last problem. Can you see the resemblance? This like a generalization that is easier in one sense (no limitation on the number of occurrences of one planet) but harder on another sense (since we now don't simple use two characters to form sequences, but a list of planets).
- The code is very similar but instead of going to the '0' and '1' recursive case, you now need to traverse the list and do a recursive case for each element
6) Generating quantities with coins [main]
![]()
For this exercise you will be solving the problem [IP088] Intergalatic Shopping.
Read the statement, code and try to submit an Accepted solution. Don't forget to test first on your computer!
This problem has similarities with [IP070], but here we have a generalization (and we can only use each coin once).
Its essence is generating all the possible subsets of coins, and subset generation was directly given in the lecture. See the code and try to understand it:
# recursive function # lst: elements that we still can add to the current subset # cur: current subset being built def subsets_rec(lst, cur): if len(lst) == 0: return [cur] # base case l1 = subsets_rec(lst[1:], cur + [lst[0]]) # recursive case 1: add 1st element l2 = subsets_rec(lst[1:], cur) # recursive case 2: don't add it return l1 + l2 # combine recursive cases # main function that calls auxiliary recursive function def subsets(lst): return subsets_rec(lst, []) print(subsets([1,2,3])) # generate all subsets of [1,2,3]
Here is the recursive tree (with the method name simplified to ss) showing the calls being made in thisrecursive function:
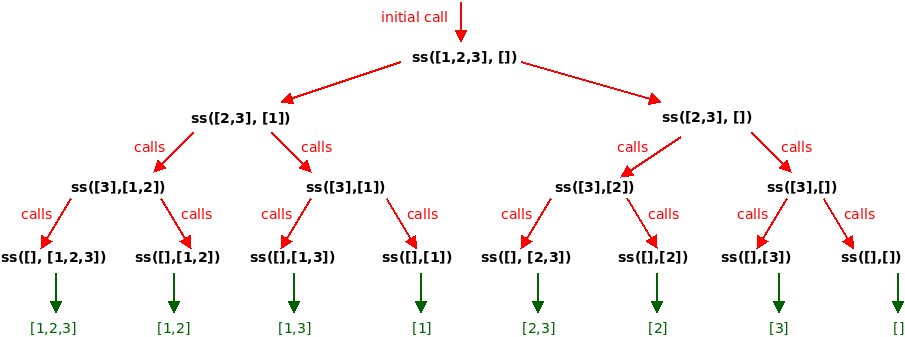
After understanding it, you are ready to implement this method.
- It's essentially the same problem, but here you need to keep track of the sum (e.g. add another parameter to the function)
- On the base case you can add the sum to a set, so that you just save unique quantities
- Another (slightly less eficient) would be to simply generate the subsets and then process them (i.e., sum them)
Do you want to continue your adventure on the world of Westeros? Here are more exercises 🙂
7) A TSP brute force approach
![]()
For this exercise you will be solving the problem [IP089] Delivery Route.
Read the statement, code and try to submit an Accepted solution. Don't forget to test first on your computer!
- Essentially the problem asks for the permutations. Can you generate them recursively?
8) Generating numbers
![]()
For this exercise you will be solving the problem [IP090] Eccentric Numbers.
Read the statement, code and try to submit an Accepted solution. Don't forget to test first on your computer!
- This problem is similar to other you did in this class
- If you want to keep the "current" number, how to add a digit? If the number is n, to add a digit d you only need to create a new number n*10 + i (e.g. n=25, d=3, new number = 25*10 +3 = 253)
9) Generating with constrainsts
![]()
For this exercise you will be solving the problem [IP091] Dinner Trouble.
Read the statement, code and try to submit an Accepted solution. Don't forget to test first on your computer!
- Can you do one totally by yourself? 😁
Congratulations! 🎉 You've successfully tackled all the problems with precision and creativity. Your journey through these challenges has been nothing short of impressive - like a true coding master navigating the vast galaxy of Recursion and Python! 🚀🐍
Now, the final frontier awaits: Dr. Zoidberg's queen-placement conundrum. It’s a chessboard-sized (classic) challenge, a test of strategy, recursion, and a touch of elegance. But with your skills and determination, this is just another puzzle waiting to be solved. 💡♟️
So go forth, conquer Zoidberg’s problem, and show that your brilliance shines even in the farthest reaches of logic. Good luck, and as Zoidberg might say: "Hooray for you!"
![]()
For this exercise you will be solving the problem [IP092] Chess Puzzle
Read the statement, code and try to submit an Accepted solution to the following problem. Don't forget to test first on your computer!
Happy coding! 😊