In geometry, the relationship between circles can be interesting, especially when analyzing their positions relative to each other.
In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of October 26th
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #03 exercise sheet]
In geometry, the relationship between circles can be interesting, especially when analyzing their positions relative to each other.
Write a program that takes the radii and centers of two circles and determines whether they are tangent.
The input consists of six floating-point numbers:
The output should be a single line indicating whether the circles are tangent or not, formatted as follows:
"The circles are tangent.""The circles are not tangent."The following limits are guaranteed in all the test cases that will be given to your program:
| 0 < r1, r2 <= 100 | Radii of the circles | |
| -100 <= x1, x2, y1, y2 <= 100 | xy coordinates of the circle centers |
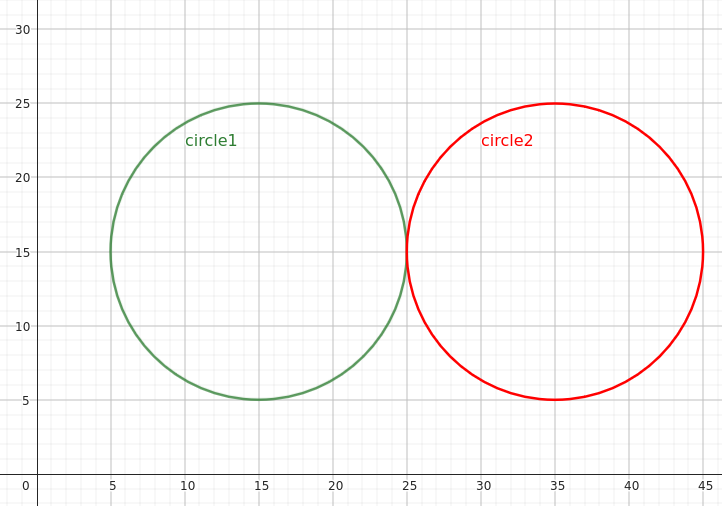
| Example Input 1 | Example Output 1 |
10 15 15 10 35 15 |
The circles are tangent. |
The first example corresponds to the following figure:
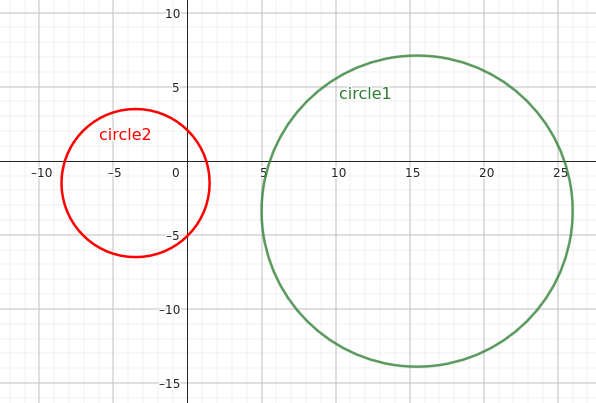
| Example Input 2 | Example Output 2 |
10.5 15.5 -3.4 5 -3.5 -1.5 |
The circles are not tangent. |
The second example corresponds to the following figure:
| Example Input 3 | Example Output 3 |
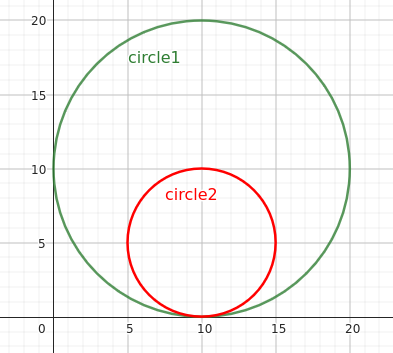
10 10 10 5 10 5 |
The circles are tangent. |
The third example corresponds to the following figure:
