In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of November 23rd
(this exercise will still be available for submission after that deadline, but without counting towards your grade)
[to understand the context of this problem, you should read the class #06 exercise sheet]

In this problem you should submit a function as described. Inside the function do not print anything that was not asked!

[IP058] Pascal Triangle

Professor Frink, Springfield's eccentric and brilliant scientist, is hard at work in his cluttered laboratory, surrounded by beakers bubbling with mysterious liquids and gadgets that seem to have a mind of their own. Today, he’s feeling particularly inspired and has decided to delve into one of his favorite mathematical topics: Pascal's Triangle. Known for its fascinating properties in combinatorics and number theory, Frink sees it as the perfect blend of math and magic.

As he jots down ideas for his next lecture, he envisions demonstrating Pascal's Triangle to his students at Springfield Elementary. Frink knows that the triangle is not only visually captivating, but also offers a plethora of applications, from probability theory to binomial expansions. He imagines the look of awe on his students' faces when they realize how each number is the sum of the two numbers directly above it.

The Problem

Write a function pascal(n) that given an integer n returns a list containing the n-th row of the pascal's triangle:

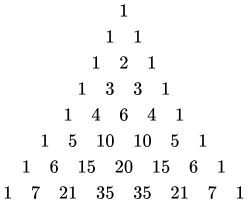
Constraints

The following limits are guaranteed in all the test cases that will be given to your program:

print(pascal(1))
print(pascal(2))
print(pascal(3))
print(pascal(4))
print(pascal(5))

[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]