This problem is a Mooshak version of a UVA Online Judge Problem.

[PC044] Number Maze

Consider a number maze represented as a two dimensional array of numbers comprehended between 0 and 9, as exemplified below. The maze can be traversed following any orthogonal direction (i.e., north, south, east and west). Considering that each cell represents a cost, then finding the minimum cost to travel the maze from one entry point to an exit point may pose you a reasonable challenge.

Your task is to find the minimum cost value to go from the top-left corner to the bottom-right corner of a given number maze of size \(N \times M\).

Input

The input file contains several mazes. The first input line contains a positive integer \(T\) defining the number of mazes that follow. Each maze is defined by: one line with the number of rows, \(N\) ; one line with the number of columns, \(M\) ; and \(N\) lines, one per each row of the maze, containing the maze numbers separated by spaces.

Output

For each maze, output one line with the required minimum value.

Constraints

Example Input Example Output 
3
4
5
0 3 1 2 9
7 3 4 9 9
1 7 5 5 3
2 3 4 2 5
1
6
0 1 2 3 4 5
6
6
1 1 1 1 9 9
9 3 8 9 9 9
1 2 9 9 9 9
1 9 1 1 1 9
1 9 1 9 1 9
1 1 1 9 1 1

24
15
20

Example Explanation

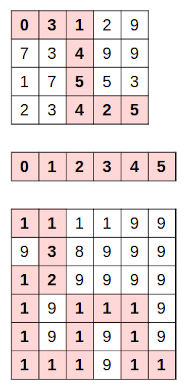
Paths with the minimum cost of 24, 15 and 20 in the first, second and third mazes are indicated below:

Competitive Programming (CC3032) 2025/2026
DCC/FCUP - University of Porto