This problem is a Mooshak version of an old Ibero-American Olympiads in Informatics problem.
[PC045] Complicated Traffic
 One of the biggest problem of Rafael's city is its complicated car
traffic. Every day he goes from home to work during the rush hour and
a lot of time is spent completely stopped in the traffic, something
which really irritates him. Because of that, Rafael decides to
carefully plan the best path to follow.
One of the biggest problem of Rafael's city is its complicated car
traffic. Every day he goes from home to work during the rush hour and
a lot of time is spent completely stopped in the traffic, something
which really irritates him. Because of that, Rafael decides to
carefully plan the best path to follow.
All the years he spent driving in the city have allowed him to make
a detailed map with traffic information. For simplifying, Rafael
decided to numerate the several city localizations with numbers from 0
to N-1, with his house always on position 0 and the work on position
N-1. The map defines roads between a pair of positions, indicating the
respective average car velocity when following that road. Note that
all roads allow circulation in both ways. Given a path, its final
value is equal to the smallest average velocity on of its constituent
roads.
The following figure illustrates a path between 0 (house)
and 8 (work). This path goes trough positions 0, 2, 4, 6 e 8,
in this order, and has a value of 22 Km/h, the minimum of the average
velocities of its roads, which are 40, 22, 28 and 50.

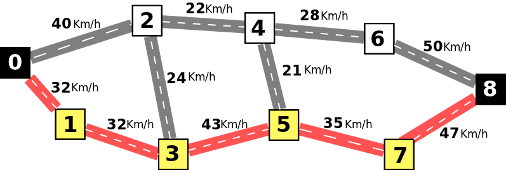
We can do better if we follow a different path, indicated in the
following figure, which has a value of 32 Km/h, larger than the path before:
Rafael knows that the mayor has some money available for renovating
some of the roads. A renovated road becomes an avenue with two lanes
in each way, which effectively doubles its average velocity. For
instance, if the road between 2 and 3 is renovated, its average
velocity would become 48 Km/h, and the following path of value 35 Km/h
(better than the ones shown before) would become possible:

In reality, the mayor will have money for renovating
at most K roads. Since Rafael thinks that its own path is very
important, he decides to send the mayor a letter, explaining the roads
that should be renovated to allow him the best possible path. For
instance, if K was 1, the scenario explained on the last figure would
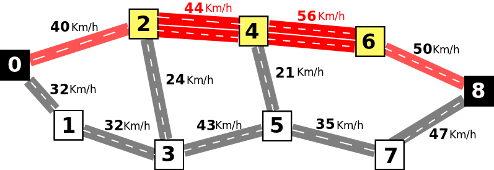
be the best possible. If K was 2, than the best would be to renovate
the roads between 2 and 4, and between 4 and 6, allowing for a path of
value 40Km/h, as illustrated on the following figure:
And for a general case? Which roads should be renovated to allow
the best possible path for Rafael?
The Problem
Given a map with N positions, a set of E roads, with
average car velocities between A and B defined
by VA,B and a number K of roads that we can
renovate, your task is to compute the value of the best possible path
for going from position 0 (the house) to position N-1 (the work),
after at most K renovations are made.
Input
The first line contains a single integer N, the number of
map positions. The second line contains a single integer E, the number of existing roads.
Then come E lines, each one containing three integers A B
VA,B, separated by a single space, indicating that
there exists a road between A and B with average
velocity of VA,B. The roads can come in any order
and there are never two roads between the same pair of
positions. There are no direct roads from a position to itself and there is
always at least one path between 0 and N-1.
Finally, the last line contains a single integer K, the
number of roads that can be renovated.
Output
A single line containing one integer representing the value of the
best possible achievable path by doing at most K renovations.
The value of a path its the minimum average velocity of one of its
roads. The best path is the one with the largest possible value. Note
that you can choose the renovations that will give origin to the best
path and that a single road can only be renovated once. If K is zero,
then the result corresponds to the best possible path without any road
renovation.
Constraints
The following limits are guaranteed for all the test cases that
will be used for evaluating your program:
| 2 ≤ N ≤ 5 000 |
|
Number of positions in the map |
| 1 ≤ E ≤ 50 000 |
|
Number of roads |
| 1 ≤ VA, B ≤ 200 |
|
Average velocity of a single road |
| 0 ≤ K ≤ 20 |
|
Amount of possible road renovations |
| Example Input 1 |
Example Output 1 |
9
11
0 2 40
2 4 22
4 6 28
6 8 50
0 1 32
1 3 32
3 5 43
5 7 35
7 8 47
2 3 24
4 5 21
1
|
35
|
| Example Input 2 |
Example Output 2 |
9
11
0 2 40
2 4 22
4 6 28
6 8 50
0 1 32
1 3 32
3 5 43
5 7 35
7 8 47
2 3 24
4 5 21
2
|
40
|
Competitive Programming (CC3032) 2025/2026
DCC/FCUP - University of Porto
 One of the biggest problem of Rafael's city is its complicated car
traffic. Every day he goes from home to work during the rush hour and
a lot of time is spent completely stopped in the traffic, something
which really irritates him. Because of that, Rafael decides to
carefully plan the best path to follow.
One of the biggest problem of Rafael's city is its complicated car
traffic. Every day he goes from home to work during the rush hour and
a lot of time is spent completely stopped in the traffic, something
which really irritates him. Because of that, Rafael decides to
carefully plan the best path to follow.



