All-Pairs Shortest Paths
Objectivo
Familiarizar os alunos com a sincronização e comunicação entre
processos em arquitecturas multiprocessador, através da utilização de
spinlocks e do mapeamento de ficheiros em memória partilhada.
Descrição
O problema que se pretende resolver consiste em encontrar o conjunto
de todos os caminhos mais curtos entre pares de nós de um determinado
grafo. Este problema é conhecido na literatura por all-pairs
shortest paths.
A ideia é a seguinte: dado um grafo dirigido G = (V,E) em que V é o
conjunto de nós e E é o conjunto de ligações entre os nós, pretende-se
determinar para todos os pares de nós (vi,vj) o tamanho do menor
caminho que começa em vi e termina em vj. Um caminho não é nada mais
do que uma sequência de ligações, em que o nó de destino e o nó de
origem de duas ligações consecutivas da sequência são o mesmo. Uma
ligação pode ser vista como um tuplo da forma < vi, vj, t > em que
vi é o nó de origem, vj é o nó de destino e t é o tamanho da ligação
entre os nós. A soma dos tamanhos das ligações de um caminho definem o
tamanho do caminho.
Implementação
Um grafo dirigido com V nós pode ser representado por uma matriz D1 de
dimensão NxN (N = 6 no exemplo que se segue) em que cada elemento
(i,j) da matriz corresponde ao tamanho da ligação que liga o nó vi ao
nó vj. A não existência de qualquer ligação entre um determinado par
de nós pode ser representado pelo valor zero.

A solução do problema pode ser igualmente representada por uma matriz
Df de dimensão NxN em que cada elemento (i,j) da matriz corresponde ao
menor tamanho dos caminhos que começam em vi e terminam em vj.

O algoritmo de Floyd-Warshall permite obter a matriz Df a partir da
matriz D1 utilizando uma forma adaptada de multiplicação de matrizes,
em que as operações de multiplicação e soma são substituídas pelas
operações de soma e mínimo, respectivamente. Utilizando essa forma
adaptada de multiplicação podemos obter a matriz Df construindo
sucessivamente matrizes D2 = D1xD1, D4 = D2xD2, D8 = D4xD4, ..., Df =
DgxDg em que f >= N e g < N.
A multiplicação de matrizes com a mesma dimensão N x N pode ser
eficientemente implementada em ambientes de memória partilhada
particionando a matriz em P submatrizes de dimensões M x N, em que P é
o número de processos disponíveis e M = N / P, e atribuindo o cálculo
de cada submatriz a cada um dos P processos. Note que esta partição
apenas pode ser aplicada se P dividir N.
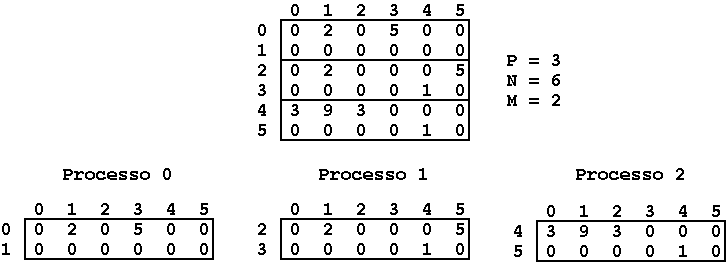
O cálculo de cada matriz Di+1 do algoritmo de Floyd-Warshall é feito
iterativamente sendo cada processo responsável pelo cálculo da
submatriz respectiva. No final de cada passo i, os processos
sincronizam entre si, actualizam a matriz Di com os resultados obtidos
nas suas submatrizes e iniciam o passo i+1 a partir da nova matriz
Di+1.
Input e Output
A aplicação a desenvolver deverá aceitar como entrada de dados um
ficheiro com a descrição do grafo a considerar. Essa descrição deverá
seguir o seguinte padrão: a primeira linha indica o inteiro N que
representa o número de nós do grafo, enquanto que as seguintes N
linhas indicam a matriz que representa as ligações entre todos os
pares de nós do grafo. Segue-se o ficheiro que descreve o grafo do
exemplo apresentado:
6
0 2 0 5 0 0
0 0 0 0 0 0
0 2 0 0 0 5
0 0 0 0 1 0
3 9 3 0 0 0
0 0 0 0 1 0
Se a dimensão da matriz não for compatível com o número de processos
indicados então deverá ser apresentada uma mensagem de erro e a
execução deve ser cancelada.
Como resultado a aplicação deverá escrever as N linhas da matriz que
representa o menor tamanho dos caminhos entre todos os pares de nós do
grafo. Para o grafo do exemplo, o resultado a obter seria o seguinte:
0 2 9 5 6 14
0 0 0 0 0 0
9 2 0 14 6 5
4 6 4 0 1 9
3 5 3 8 0 8
4 6 4 9 1 0
O ficheiro de entrada de dados deverá ser lido do standard
input e o resultado deverá ser escrito para o standard
output (carregue aqui para obter um
conjunto de exemplos de teste).
Resultados
A aplicação a desenvolver deverá utilizar spinlocks (carregue aqui para obter o ficheiro .h com as macros de
locking) para sincronizar as operações de escrita sobre as matrizes Di
e o mapeamento de ficheiros em memória partilhada para representar
essas matrizes (carregue aqui para obter o
esqueleto do código da aplicação).



