Trabalho I: All-Pairs Shortest Paths

Objectivo

Permitir que os alunos adquiram uma maior sensibilidade e conhecimento prático do funcionamento de um ambiente de programação distribuído através da utilização da ferramenta de programação MPI.

Descrição

O problema que se pretende resolver consiste em encontrar o conjunto de todos os caminhos mais curtos entre pares de nós de um determinado grafo. Este problema é conhecido na literatura por all-pairs shortest paths.

A ideia é a seguinte: dado um grafo dirigido G = (V,E) em que V é o conjunto de nós e E é o conjunto de ligações entre os nós, pretende-se determinar para todos os pares de nós (vi,vj) o tamanho do menor caminho que começa em vi e termina em vj. Um caminho não é nada mais do que uma sequência de ligações, em que o nó de destino e o nó de origem de duas ligações consecutivas da sequência são o mesmo. Uma ligação pode ser vista como um tuplo da forma < vi, vj, t > em que vi é o nó de origem, vj é o nó de destino e t é o tamanho da ligação entre os nós. A soma dos tamanhos das ligações de um caminho definem o tamanho do caminho.

Implementação

Um grafo dirigido com V nós pode ser representado por uma matriz D1 de dimensão NxN (N = 6 no exemplo que se segue) em que cada elemento (i,j) da matriz corresponde ao tamanho da ligação que liga o nó vi ao nó vj. A não existência de qualquer ligação entre um determinado par de nós pode ser representado pelo valor zero.

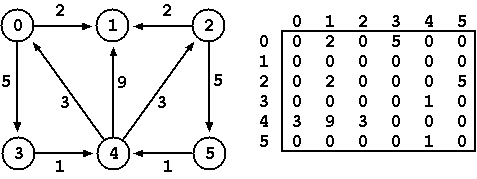
A solução do problema pode ser igualmente representada por uma matriz Df de dimensão NxN em que cada elemento (i,j) da matriz corresponde ao menor tamanho dos caminhos que começam em vi e terminam em vj.

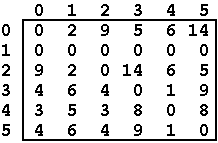
O algoritmo de Floyd-Warshall permite obter a matriz Df a partir da matriz D1 utilizando uma forma adaptada de multiplicação de matrizes, em que as operações de multiplicação e soma são substituídas pelas operações de soma e mínimo, respectivamente. Utilizando essa forma adaptada de multiplicação podemos obter a matriz Df construindo sucessivamente matrizes D2 = D1xD1, D4 = D2xD2, D8 = D4xD4, ..., Df = DgxDg em que f >= N e g < N.

A multiplicação de matrizes com a mesma dimensão pode ser eficientemente implementada em ambientes distribuídos utilizando o algoritmo de Fox. No entanto, a aplicação do algoritmo de Fox nem sempre é possível pois depende da dimensão das matrizes a multiplicar e do número de processos disponíveis. Para matrizes de dimensão NxN e P processos disponíveis no sistema, deve existir um inteiro Q tal que P = Q * Q e N mod Q = 0. O algoritmo de Fox divide as matrizes de dimensão NxN em P sub-matrizes de dimensão (N/Q)x(N/Q) e atribui cada uma delas aos P processos disponíveis no sistema.

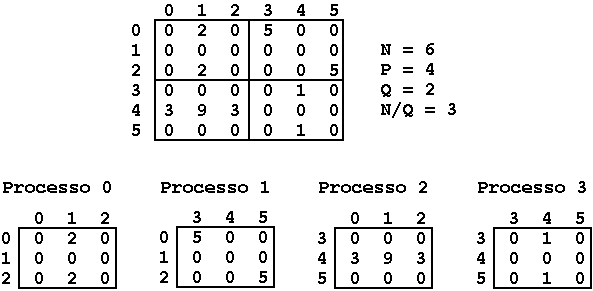
Para calcular o resultado da multiplicação da sua sub-matriz, cada processo, apenas necessita de trocar informação com os processos da mesma linha e da mesma coluna de sub-matrizes que a sua, o que permite reduzir o tamanho e número de mensagens a trocar entre os processos envolvidos (consulte as páginas 29 e 30 do A User's Guide to MPI para uma descrição mais detalhada do algoritmo de Fox). A aplicação sucessiva do algoritmo de Fox permite calcular as matrizes D2, D4, ..., Df do algoritmo de Floyd-Warshall e obter assim a matriz que soluciona o nosso problema.

Input e Output

A aplicação a desenvolver deverá aceitar como entrada de dados um ficheiro com a descrição do grafo a considerar. Essa descrição deverá seguir o seguinte padrão: a primeira linha indica o inteiro N que representa o número de nós do grafo, enquanto que as seguintes N linhas indicam a matriz que representa as ligações entre todos os pares de nós do grafo. A descrição do grafo do exemplo seria a seguinte: 
6
0 2 0 5 0 0
0 0 0 0 0 0
0 2 0 0 0 5
0 0 0 0 1 0
3 9 3 0 0 0
0 0 0 0 1 0
No caso da dimensão da matriz e do número de processos disponíveis não serem compatíveis com os requisitos do algoritmo de Fox, deverá ser apresentada uma mensagem de erro e a execução deve ser cancelada.

Como resultado a aplicação deverá escrever as N linhas da matriz que representa o menor tamanho dos caminhos entre todos os pares de nós do grafo. Para o grafo do exemplo, o resultado a obter seria o seguinte: 

0 2 9 5 6 14
0 0 0 0 0 0
9 2 0 14 6 5
4 6 4 0 1 9
3 5 3 8 0 8
4 6 4 9 1 0
O ficheiro de entrada de dados deverá ser lido do standard input e o resultado deverá ser escrito para o standard output (carregue aqui para obter um conjunto de exemplos de teste).

O Que Entregar?

Um ficheiro .tar que inclua: O código deve compilar e executar nas máquinas disponibilizadas para o efeito. Uma boa estruturação e legibilidade do código será valorizada.

Prazos

O trabalho deve ser entregue via web até às 16 horas do dia 9 de Novembro de 2007, sendo a sua demonstração feita na semana seguinte em horário a definir.