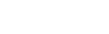 (6)
(6)In a recent paper Cestnik [1990] has drawn the attention to some earlier work concerned with the issue of estimating the probability of success, given n successes in N trials. According to Good[1965] the mathematical expectation of the probability of a success in the next trial is equal to:
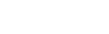 (6)
(6)
where
a, b are parameters. Moreover a + b = m,
where the exact value of m depends on the level of noise.
The expression shown above can be rewritten as follows:
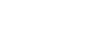 (7)
(7)
If a=1 and m=2 we get Laplace<<s law of succession:
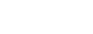 (8)
(8)
As Good has shown parameter a can be estimated using a = m * p(C), where p(C) represents the prior probability of class C which can be calculated using Laplace<<s law of succession.
If we apply these methods to the problem of estimating accuracy of rule R we get:
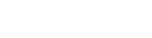 (9)
(9)
where
CR represents the number of correctly classified
cases
and CR + ERR the total number of cases.
If a=1 and m=2 we get Laplace<<s law of succession:
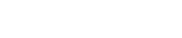 (10)
(10)
If we use Good<<s method we get:
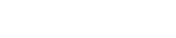 (11)
(11)
where
a = m * (NC + 1) / (NTOT + 2)
Let us consider the example discussed earlier:
rule(1-5, metastase <-- earlyuptakein = no & defectinnode = lac_central, 15, 3).
The number of classified cases (CR) is 15 and number of misclassifications (ERR) is 3, and R is 1-5. Assuming that m is 2 and that there are 30 examples of metastase (NC =30) in a total of 100 cases available, the value of parameter a will be
a = 2 * (30 + 1) / (100 + 2) = 62 / 102 = 0.608
As CR is 15 and ERR is 3, then
QR ,Good = (15 + 0.608) / ((15 + 3) + 2) = 15.608 / 20 = 0.708,
QR,Laplace = (15 + 1 ) / ((15 + 3) + 2) = 16 / 20 = 0.800.
Note that it does not make much sense to compare the values of QR calculated using different methods. It is more important to see how different methods affect performance gains. We have conducted experiments to enable us to do such comparisons. The following table summarizes our results. All the figures are means calculated on the basis of 20 measurements.
Table 4. Effects of Different Methods of Calculating QR on Performance Gains of the Integrated Theory
5 10 15 20 25 30 examples
QR,Torgo 13.7 14.7 14.3 15.8 15.4 12.9 %
QR,Laplace 16.4 13.0 15.5 14.0 12.3 12.2
QR,Good 12.5 8.5 7.8 10.9 11.3 11.6
The results indicate that the method of Torgo is superior to the other two methods considered here. The method based on Laplace<<s law of succession performs also reasonably well, but the more complex variant based on Good<<s probability estimates is surprisingly weaker.
We believe that Torgo<<s method works well, as it takes into account both rule accuracy and class coverage. We recall that rule accuracy is affected by errors of commission and class coverage by errors of omission (see Section 2). Both types of errors are thus taken into account in the calculation of rule quality. This is perhaps the secret of this formula<<s success.
In the next section we describe some of the shortcomings of our approach and some possible extensions.