 |
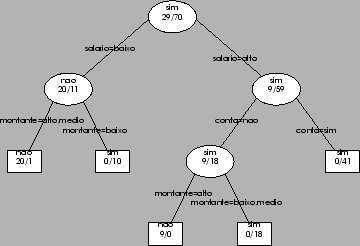
| Figura 3: Um exemplo de uma árvore de decisão. |
O R possuí uma gama bastante variada de métodos que podem ser usados para obter modelos para problemas de classificação como por exemplo o da concessão de crédito que temos vindo a usar. Um desses métodos é normalmente conhecido como árvores de decisão. Antes de vermos como obter uma árvore de decisão em R, vejamos em que consistem esses modelos e como podem ser usados para tomar decisões. A Figura 3 mostra um exemplo de uma árvore de decisão para o problema da concessão de crédito.
Uma árvore de decisão consiste numa hierarquia de testes a algumas das variáveis envolvidas no problema de decisão, que no nosso exemplo são as variáveis montante, idade, salário e conta. A árvore pode ser ``lida'' a partir do teste encontrado na parte superior da mesma, normalmente chamado o nó raiz da árvore. Em concreto, se pretendêssemos usar a árvore da Figura 3 para tomar uma decisão para um novo cliente do banco, a primeira coisa para que deveríamos olhar, de acordo com esta árvore de decisão, seria para o seu salário. Se este fosse baixo, então de acordo com a árvore deveríamos verificar qual o montante pedido. Se for um montante alto ou médio então a decisão aconselhada pela árvore é não conceder crédito. Se por outro lado o montante fosse baixo então já deveríamos conceder crédito ao cliente. Ou seja, para usar uma árvore deste tipo para tomar decisões, começamos por fazer o teste do nó raiz. Se for verdadeiro seguimos para o ramo esquerdo da árvore e fazemos o teste que aí se encontra, se for falso seguimos o ramo direito, e assim sucessivamente até chegarmos a um nó terminal (normalmente conhecidos por folhas da árvore), onde temos a decisão do modelo para o caso em análise.
As árvores de decisão como a da Figura 3 podem ser ``lidas'' como um conjunto de regras de decisão. Por exemplo o caminho desde o nó raiz, seguindo sempre o ramo esquerdo até encontrar uma folha, corresponde à regra,
Isto quer dizer que seria possível traduzir uma árvore de decisão para um conjunto de regras de decisão, e assim usar um procedimento semelhante ao seguido na Secção 2.1.1 para as implementar como uma função que toma decisões para novos casos.
Vejamos agora como construir uma árvore de decisão no R. Conforme já mencionamos anteriormente, a significância da amostra usada para obter o modelo é essencial para termos um mínimo de garantias da representatividade do modelo construído. Assim, não faz grande sentido obter uma árvore de decisão usando meia dúzia de exemplos de decisões. De facto, quanto maior a amostra usada melhor. Apesar destas considerações, para o efeito de mostrar como se obtém uma árvore em R, é indiferente o tamanho da amostra usada. Assim, vamos criar um pequeno data frame com exemplos de decisões (por exemplo semelhantes às apresentadas na Tabela 1 da página ![]() ). Podemos usar o editor de data frames do R para criar um data frame com os exemplos, ou em alternativa podemos usar a possibilidade que o R nos dá de ir buscar informação à Internet, desde que obviamente o computador em causa esteja ligado a esta rede. Vejamos como proceder neste segundo caso,
). Podemos usar o editor de data frames do R para criar um data frame com os exemplos, ou em alternativa podemos usar a possibilidade que o R nos dá de ir buscar informação à Internet, desde que obviamente o computador em causa esteja ligado a esta rede. Vejamos como proceder neste segundo caso,
> download.file('http://www.liacc.up.pt/~ltorgo/Ensino/FEP/AnaliseDados/credito.Rdata','exp.data')
trying URL `http://www.liacc.up.pt/~ltorgo/Ensino/FEP/AnaliseDados/credito.Rdata'
Content type `text/plain' length 2661 bytes
opened URL
downloaded 2661 bytes
> dados <- read.csv('exp.data')
> dados
montante idade salario conta emprestimo
1 medio junior baixo sim nao
2 medio junior baixo nao nao
3 baixo junior baixo sim sim
4 alto media baixo sim sim
5 alto senior alto sim sim
...
...
A primeira instrução apresentada acima é uma chamada à função download.file do R que pode ser usada para fazer o download de um ficheiro da Internet a partir do seu endereço (URL), colocando o resultado num ficheiro local ao computador onde se está a executar o R. Neste caso indicamos um URL que foi criado para este efeito, e que é suposto conter um ficheiro de texto com uma série de exemplos de decisões. O resultado do download é colocado num ficheiro que resolvemos chamar ``exp.data''.
A segunda instrução usa a função read.csv para ler o conteúdo do ficheiro ``exp.data'' para um data frame. Esta função pode ser usada para ler o conteúdo de ficheiros de texto do tipo CSV. Este tipo de ficheiros contém informação tabular com a informação distribuída por linhas, e com os valores em cada linha separados por vírgulas. Este tipo de ficheiros pode ser gerado pela maioria dos programas como por exemplo o Access, o Excel, etc. Para termos uma melhor ideia do seu conteúdo, apresentam-se em seguida as primeiras linhas do ficheiro ``exp.data'',
montante,idade,salario,conta,emprestimo medio,junior,baixo,sim,nao medio,junior,baixo,nao,nao baixo,junior,baixo,sim,sim alto,media,baixo,sim,sim ...
Com a instrução read.csv() usada da forma apresentada acima, a primeira linha deste ficheiro é interpretada como os nomes a dar às colunas do data frame que será criado, e as linhas sucessivas como o conteúdo desse data frame. Isso mesmo pode ser confirmado pedindo ao R para mostrar o conteúdo do objecto dados.
Após termos um conjunto de exemplos de crédito num data frame, estamos em condições de obter uma árvore de decisão. As seguintes instruções fazem isso mesmo,
> library(rpart)
> árvore <- rpart(emprestimo ~ ., dados)
> árvore
n= 99
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 99 29 sim (0.29292929 0.70707071)
2) salario=baixo 31 11 nao (0.64516129 0.35483871)
4) montante=alto,medio 21 1 nao (0.95238095 0.04761905) *
5) montante=baixo 10 0 sim (0.00000000 1.00000000) *
3) salario=alto 68 9 sim (0.13235294 0.86764706)
6) conta=nao 27 9 sim (0.33333333 0.66666667)
12) montante=alto 9 0 nao (1.00000000 0.00000000) *
13) montante=baixo,medio 18 0 sim (0.00000000 1.00000000) *
7) conta=sim 41 0 sim (0.00000000 1.00000000) *
A primeira destas instruções carrega o package ``rpart'' que contém as funções necessárias para a obtenção de árvores de decisão no R. A segunda instrução obtém um destes modelos usando a função rpart colocando o resultado no objecto árvore. A função rpart tem dois argumentos principais. Um indica a forma do modelo a obter, e o outro os dados a usar para o obter. A forma do modelo a obter é fornecida à função usando uma sintaxe genérica de descrição de modelos que consiste, sucintamente, em indicar o nome da variável de decisão seguida do símbolo "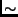 " e uma lista das variáveis que podem ser usadas no modelo para obter a decisão. Esta lista pode ser substituída pelo símbolo "." (como no exemplo acima), querendo significar que se podem usar todas as outras variáveis existentes nos dados fornecidos à função. Os dados a usar na obtenção do modelo são fornecidos no segundo argumento da função e devem ser um data frame com as colunas com nomes que estejam de acordo com os nomes de variáveis referidos na forma do modelo.
" e uma lista das variáveis que podem ser usadas no modelo para obter a decisão. Esta lista pode ser substituída pelo símbolo "." (como no exemplo acima), querendo significar que se podem usar todas as outras variáveis existentes nos dados fornecidos à função. Os dados a usar na obtenção do modelo são fornecidos no segundo argumento da função e devem ser um data frame com as colunas com nomes que estejam de acordo com os nomes de variáveis referidos na forma do modelo.
A seguir a obter a árvore podemos pedir ao R para mostrar o conteúdo do objecto a que atribuímos o resultado. O R apresenta a árvore de decisão em forma de texto. Como veremos mais à frente vai ser também possível obter uma representação gráfica como a da Figura 3. Analisemos para já a informação dada pelo R sobre o objecto árvore. Em primeiro lugar o R indica-nos o número de casos usados para obter o modelo. Em seguida, são apresentadas uma série de linhas que representam os diferentes testes e nós da árvore. Estes são apresentados seguindo uma certa indentação e com um número associado, com o objectivo de melhor percebermos a hierarquia dos testes. Maior indentação significa que o teste / nó se situa num nível mais abaixo na árvore (ajuda a compreender a informação olhar para a Figura 3 em paralelo, que é uma representação gráfica da mesma árvore). Assim, neste exemplo concreto a primeira linha identificada com o número 1 dá-nos a informação respeitante ao nó raiz da árvore, antes de efectuar qualquer teste a uma variável. De acordo com essa informação no nó raiz, antes de sabermos / testarmos o valor de qualquer variável, a melhor decisão seria ``sim'' (i.e. conceder crédito). Esta decisão é sustentada pelo facto de dos 99 exemplos dados ao R só 29 serem da ``classe'' não, o que leva a uma probabilidade de 29.9% de qualquer cliente ser um caso de ``não conceder'' crédito, e uma probabilidade de 70.7% de ser uma caso de ``sim, conceder'' crédito. Estas probabilidades são os números apresentados entre parênteses. Deste nó raíz temos duas derivações consoante o valor da variável salário. Estas derivações estão identificadas pelos números 2 e 3, e correspondem ao nível seguinte de identação. Dos 99 casos fornecidos ao R, 31 têm a propriedade ``salário = baixo'' e nestes a classe maioritária é ``não'' conceder crédito, sendo que só 11 dos 31 correspodem a situações onde os peritos decidiram dar crédito. Para estes 31 casos o teste seguinte é o valor do montante pedido. Se este for alto ou médio, então atinge-se uma decisão (o R assinala isso colocando um ``*'' na respectiva linha), que neste caso é não conceder crédito. Esta decisão é suportada pelo facto de dos 21 casos com montante alto ou médio só 1 ter recebido uma decisão de conceder crédito pelos peritos humanos. Em resumo, usando os números e a identação é possível ficar com uma ideia da forma do modelo de decisão obtido com a função rpart.
A criação de uma representação gráfica de uma árvore de decisão, é um processo de duas fases em R. Em primeiro lugar desenha-se a árvore e depois coloca-se o texto no desenho. As instruções seguintes fazem isso mesmo,
> plot(árvore) > text(árvore)
O resultado obtido desta forma é um pouco fraco em termos gráficos. Conseguem-se melhores resultados jogando um pouco com os muitos parâmetros destas duas funções. No sentido de evitarmos estarmos a escrever estes parâmetros sempre que queiramos visualizar uma árvore de decisão, vamos criar um função para esse efeito,
> mostra.arvore <- function(árvore) {
+ plot(árvore,uniform=T,branch=0)
+ text(árvore,digits=3,cex=0.65,font=10, pretty=0,fancy=T,fwidth=0,fheight=0)
+ }
> mostra.arvore(árvore)
Como se pode ver pela amostra da Figura 3 (que também foi produzida com estas duas funções, mas com parâmetros diferentes), pode-se fazer ainda muito melhor manipulando os parâmetros destas funções, no entanto tais detalhes saiem fora do âmbito desta cadeira.
Após a obtenção de um modelo de decisão deste tipo, a pergunta óbvia que surge é,
Qual a confiança que podemos ter na performance deste modelo?
Uma das formas mais práticas de responder a esta questão consiste em testar o modelo usando para isso novos casos de decisões dos peritos humanos, e contabilizando as decisões incorrectas, quando comparadas com as dos peritos humanos, cometidas pela árvore de decisão.
Uma forma de simular a existência de mais casos para testarmos o nosso modelo, consiste em dividir os casos que possuímos em dois sub-conjuntos: uma para obter o modelo; e outro para o testar. Vejamos como fazer isso em R,
> amostra.modelo <- sample(1:nrow(dados),as.integer(0.7*nrow(dados))) > dados.modelo <- dados[amostra.modelo,] > dados.teste <- dados[-amostra.modelo,]
O objectivo da primeira instrução é obter uma amostra aleatória de números entre 1 e o número de linhas do data frame dados. O tamanho dessa amostra corresponde a 70% do número de linhas do objecto dados. A função sample() permite obter este tipo de resultados. Por exemplo, se pretendessemos obter um vector com 3 números aleatórios entre 1 e 10, bastaria fazer,
> v <- sample(1:10,3)
Uma vez obtido um vector com um conjunto de número aleatórios entre 1 e o número de casos que possuímos, podemos usar este vector (amostra.modelo) para indexar o data frame com todos os casos, e deste modo obter um novo data frame contendo um sub-conjunto aleatório dos casos disponíveis. Usando as facilidades de indexação do R (c.f. Secção 1.8), podemos facilmente obter o complemento deste conjunto, isto é os casos restantes. Com estas duas amostras aleatórias, que são exclusivas, podemos construir uma árvore de decisão e depois testá-la numa amostra de casos independente, garantindo assim alguma fiabilidade às nossas estimativas da qualidade do modelo de decisão. Vejamos como proceder,
> árvore <- rpart(emprestimo ~.,dados.modelo)
> árvore
n= 69
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 69 21 sim (0.3043478 0.6956522)
2) salario=baixo 24 9 nao (0.6250000 0.3750000)
4) montante=alto,medio 16 1 nao (0.9375000 0.0625000) *
5) montante=baixo 8 0 sim (0.0000000 1.0000000) *
3) salario=alto 45 6 sim (0.1333333 0.8666667) *
> previsões.modelo <- predict(árvore,dados.teste)
> previsões.modelo
nao sim
2 0.9375000 0.0625000
5 0.1333333 0.8666667
7 0.1333333 0.8666667
8 0.9375000 0.0625000
11 0.1333333 0.8666667
...
Repare que, uma vez que usamos um conjunto de dados diferente para obter o modelo, a árvore obtida é diferente da anterior. A terceira instrução usa a função predict para obter as previsões da árvore para os casos da amostra separada para teste. Repare que o papel desta função é semelhante à função de decisão que implementamos na Secção 2.1.1, isto é, para cada casos de teste emite uma previsão. Neste caso concreto a função predict produz um data frame com tantas linhas quantos os casos de teste, e com tantas colunas quantas as decisões possíveis no problema. Para cada caso de teste a função produz a probabilidade de cada decisão. Assim, por exemplo, no primeiro caso de teste a árvore prevê não conceder crédito com cerca de 93.7% de ``confiança'' e conceder crédito com somente 6.2%.
Para calcularmos a percentagem de erros destas decisões da árvore, é preferível obter as decisões de uma outra forma,
> previsões.modelo <- predict(árvore,dados.teste,type='class') > previsões.modelo [1] nao sim sim nao sim sim sim sim sim sim sim sim sim sim sim nao sim sim sim [20] nao sim sim sim sim nao sim sim sim sim sim Levels: nao sim
Com o parâmetro ``type='class''' a função predict produz um factor com as decisões ``definitivas'' da árvore, em vez das probabilidades de cada classe (decisão). Estas previsões podem agora ser comparadas com os valores verdadeiros dos casos de teste e deste modo obter uma ideia da performance da árvore,
> table(dados.teste$emprestimo,previsões.modelo)
previsões.modelo
nao sim
nao 5 3
sim 0 22
A função table foi já apresentada anteriormente, e permite fazer a tabulação cruzada de dois factores. Neste caso concreto, estamos a comparar os valores da coluna com a decisão dos peritos humanos nos casos de teste (as previsões ``correctas''), com as previsões da árvore. A informação resultante é normalmente conhecida como a matriz de confusão das previsões do modelo. Ela diz-nos que dos 8 casos em que os peritos humanos recomendaram não conceder crédito, a árvore também recomendou o mesmo em 5 casos, mas fez a recomendação errada em 3. Por outro lado, dos 22 casos em que os peritos do banco recomendaram dar crédito, a árvore disse o mesmo para todos eles. Com esta informação é fácil calcular a percentagem de decisões erradas da árvore, uma vez que o resultado da função table é uma matriz,
> m.conf <- table(dados.teste$emprestimo,previsões.modelo) > perc.erro <- 100 * (m.conf[1,2]+m.conf[2,1]) / sum(m.conf) > perc.erro [1] 10
Em primeiro lugar colocámos o resultado da função table usada acima, num objecto chamado m.conf. Em seguida, calculamos a percentagem de previsões erradas usando a informação da matriz de confusão. A percentagem de decisões corresponde a somar todos os números da matriz que não estão na diagonal (pois estas são as decisões acertadas), e dividir esta soma pela soma total de todos os números (que de facto é o número total de decisões tomadas). Repare que a solução apresentada é específica para um problema com duas decisões possíveis, pois de contrário teríamos mais células da matriz que corresponderiam a decisões erradas.
Podemos facilitar o nosso uso futuro das árvores do R criando uma função que realize toda a parte de avaliação,
> avalia.árvore <- function(árv,dados.teste,objectivo=ncol(dados.teste)) {
+ prevs <- predict(árv,dados.teste)
+ m.conf <- table(dados.teste[,objectivo],predict(árv,dados.teste,type='class'))
+ erro <- 100*sum(m.conf[col(m.conf) != row(m.conf)]) / sum(m.conf)
+ list(previsões=prevs, matriz.confusão=m.conf, perc.erro=erro)
+ }
> resultados <- avalia.árvore(árvore,dados.teste)
> resultados
$previsões
nao sim
2 0.9375000 0.0625000
5 0.1333333 0.8666667
7 0.1333333 0.8666667
8 0.9375000 0.0625000
11 0.1333333 0.8666667
13 0.1333333 0.8666667
20 0.1333333 0.8666667
...
...
$matriz.confusão
nao sim
nao 5 3
sim 0 22
$perc.erro
[1] 10
Repare que esta função já não tem a limitação do número de decisões ser duas, mencionada acima. De facto, com a estratégia seguida conseguimos calcular a percentagem de erro qualquer que seja o número de decisões (classes). A soma dos elementos fora da diagonal pode parecer um pouco ``rebuscada''. O que fizemos foi, tirar partido das capacidades de indexação do R, e de duas funções (col() e row()) que produzem uma matriz com os números das colunas, respectivamente linhas, dos elementos de uma matriz. Assim, a leitura da construção sum(m.conf[col(m.conf) != row(m.conf)]) é: somar os elementos da matriz m.conf que estão em posições em que o número da coluna é diferente (o operador !=) do número da linha, ou seja os elementos fora da diagonal da matriz!
A função avalia.árvore tem algumas novidades em relação às que vimos anteriormente. A primeira é a forma do seu terceiro argumento. Por vezes existem situações em que uma função tem parâmetros que na maioria das vezes vão ser usados com o mesmo valor. Nestas situações, em vez de obrigar o utilizador da função a, sempre que utiliza a função, incluir esses parâmetros que quase sempre têm o mesmo valor, o R permite-nos evitar este trabalho indicando um valor por defeito para esses argumentos. Deste modo, se o utilizador não explicitar nenhum valor para esses parâmetros o R vai usar esse valor por defeito. Para indicar o valor por defeito de um argumento basta, quando se cria a função, à frente do argumento pôr um sinal igual e o valor por defeito, como acontece com o parâmetro objectivo da nossa função. Vejamos então qual a ideia no nosso exemplo concreto. Como pretendemos que a nossa função avalia.árvore funcione para qualquer problema de decisão, e não só este da concessão de crédito, não sabemos à partida qual o nome da coluna do data frame com os dados, que corresponde à variável de decisão. Assim, decidimos assumir que, se nada for dito pelo utilizador, a variável de decisão é a última coluna do data frame. Esse é o papel do parâmetro objectivo. Ele por defeito é um número que corresponde ao número de colunas do data frame. Se o utilizador estiver a testar um problema em que a variável objectivo não esteja na última coluna, então terá que o explicitar ao usar a função, como no exemplo seguinte,
> res <- avalia.árvore(outra, outros.dados, objectivo=1)
Neste exemplo o utilizador indica à função que a variável objectivo está na primeira coluna do data frame.
A outra novidade da função avalia.árvore é a de que ela dá como resultado uma lista com três componentes. A primeira componente, chamada previsões contém as decisões com respectivas probabilidades para cada caso de teste. A segunda componente, de nome matriz.confusão, contém a matriz de confusão das previsões, enquanto a terceira componente (perc.erro), a percentagem de decisões erradas do modelo.