Algorithms and Data Structures 2024/2025 (L.EIC011) - DCC/FCUP & DEI/FEUP

Practical Class #06 - Lists, Stacks and Queues
(04/11 to 08/11)

Exercises for submission

In what concerns the continuous evaluation solving exercises during the semester, the exercises you can submit in this class are:

Submission Deadline: November 23rd (submit to AED's Mooshak)

You are encouraged to talk to the professor and to your colleagues if you have difficulties. However, any more direct help you have received from other colleagues should be acknowledged in the comments of the code you submit.
After the deadline the problems will still be available on Mooshak, but the submissions will not count towards your grade.
Each class is worth 10 per cent of the grade for this component. As there will be 11 classes with submissions, you can get full marks even if you haven't done everything.
For a problem to count, you have to get all the tests right (i.e. accepted). Even if you solve all the problems, the maximum in a single class is 100 per cent.
it is guaranted that the main exercises on each class will sum to at least 100% of the class grade.

Lectures Content

This class is about applications of lists, deques, stacks and queues. It is therefore convenient that you know what was discussed on the lectures:

The exercises for this class will involve the usage of STL containers such as list, deque, stack and queue.

1. An application of lists

  1. Using STL Lists

    Start by downloading the lists_example.cpp file. Open on your editor, understand it and then compile and execute it. You should have the following output:

    3 5 7 1 
42 3 5 7 20 
42
3
5
42 5 7 20 
forty two 
a e i o u 
1 0 1

    Have a look at the documentation about the container list to see all the available methods.

  2. Solving a counting-out problem


    For this exercise you will be solving the problem [AED026] Eeny, meeny, miny, moe.
    Desired time complexity: \(O(N \times K)\)

    The problems ask you to simulate a counting-out game. Our suggestion is for you to do the following:


2. An application of stacks

  1. Using STL Stacks

    Start by downloading the stacks_example.cpp file. Open on your editor, understand it and then compile and execute it. You should have the following output:

    Stack size: 0
Stack size: 4
At the top: 8
At the top: 6
At the top: 4
At the top: 2
Stack size: 0

    Have a look at the documentation about the container stack to see all the available methods and remember how a stack works on a LIFO fashion (last-in-first-out).

  2. Combining multiple variables into one (light weight) data structure type

    Sometimes you have the need to combine several variables into one data structure. For that you can use for instance:

    Download the types_example.cpp file. Open on your editor, understand it and then compile and execute it.

    Remember that you can also use classes if you want to add functionality (methods), as you already know.

  3. Expression validation


    For this exercise you will be solving the problem [AED027] Perfect Weddings
    Desired time complexity: \(O(|E|)\)

    The problems asks you to match different parentheses (), brackets [] and curly braces {}. At its core this is a problem that can be solved by using a stack:

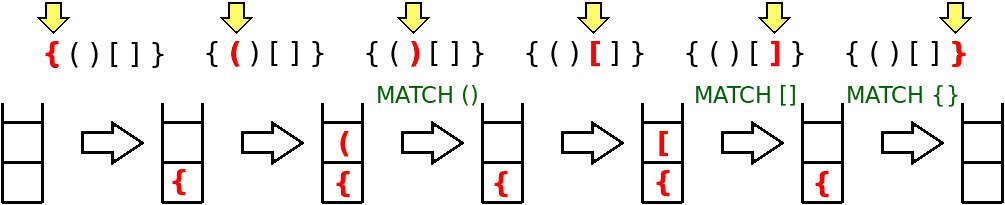
    Our suggestion is for you to use a stack as the core of your implementation:


3. An application of queues

  1. Using STL Queues

    Start by downloading the queues_example.cpp file. Open on your editor, understand it and then compile and execute it. You should have the following output:

    Queue size: 0
Queue size: 4
At the front: 2 | At the back: 8
At the front: 4 | At the back: 8
At the front: 6 | At the back: 8
At the front: 8 | At the back: 8
Queue size: 0

    Have a look at the documentation about the container queue to see all the available methods and remember how a queue works on a FIFO fashion (first-in-first-out).

  2. Round-Robin Scheduling


    For this exercise you will be solving the problem [AED028] Round-Robin
    Desired time complexity: \(O(N \times max(R_i)/T)\)

    The problems asks you to simulate round robin scheduling, which is a very well known algorithm.

    Our suggestion is for you to directly implement a simulation of the algorithm:


Extra Exercises for Consolidating your knowledge [extra]

4. Convex Hull


For this exercise you will be solving the problem [AED029] Convex Hull .
Desired time complexity: \(O(N \log N)\)

The convex hull problem (a very useful computational geometry primitive) was discussed in detail in the lectures in chapter 6 (see slides 11 to 23).

For this exercise, we propose you implement Graham's Scan algorithm, which at its core uses a stack (see slides 22 and 23).

You can use the following skeleton file as the base for you implementation and complete it: skeletonGrahamScan.cpp

5. Supermarket Queues


For this exercise you will be solving the problem [AED030] Supermarket.
Desired time complexity: \(O(N \times C)\)

For this exercise you need to simulate a more complex scenario with several queues.

The key to have an Accepted is to structure and organize your code:


Challenges Exercises [challenge]

The main idea of the challenge problems is to give you the opportunity of improving your problem solving abilities.


For this exercise you will be solving the problem [AED031] Golden Permits.

Since this is a challenge, I will not give you any hints, but if you are stuck just contact @PedroRibeiro on Discord. Feel free to also contact @PedroRibeiro to discuss your accepted solution.

This is a its essence the same problem as [AED026] Eeny, meeny, miny, moe, but now a "brute force" approach in \(O(N \times K)\) is not enough! How can you improve such that the time does not depend on \(K\) but just linearly on \(N\)?

Happy coding! 😊

Pedro Ribeiro & Ana Paula Tomás (DCC/FCUP) / Última actualização: