In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of November 23rd
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #06 exercise sheet]
[AED029] Convex Hull
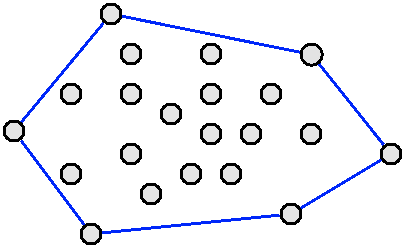 The convex
hull of a set of 2D points is the smallest convex polygon that
encloses all the points. It is a very useful geometric primitive
that can give a rough idea of the shape of the set of points. It
also serves as first preprocessing step to many other geometric
algorithms.
The convex
hull of a set of 2D points is the smallest convex polygon that
encloses all the points. It is a very useful geometric primitive
that can give a rough idea of the shape of the set of points. It
also serves as first preprocessing step to many other geometric
algorithms.
The Problem
Given a set of 2D points in general position (i.e., such that no three points are collinear), your task is to compute their convex hull.
Input
The first line contains an integer N, the number of points to consider.
The following N lines contain the points, one per line, as two space separated integers in the format Xi Yi.
It is guaranteed that the points are pairwise distinct and any three points are non-collinear, that is, they do not lie on a single line.
Output
The output should contain the number of points in the convex hull, followed by the points themselves in the same format as in the input (one per line as a pair of X Y coordinates).
The points should come in counter-clockwise order, starting with the bottom most point (the one with the smaller Y coordinate; in case of a tie in Y, choose the one with the smallest X coordinate).
Constraints
The following limits are guaranteed in all the test cases that will be given to your program:
| 3 ≤ N ≤ 500 |
|
Number of Points |
| 0 ≤ Xi, Yi ≤ 1000 |
|
Coordinates |
| Example Input |
Example Output |
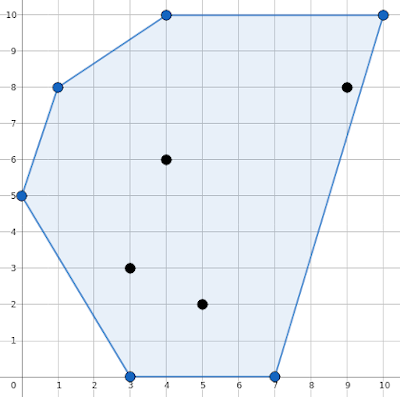
10
5 2
0 5
3 3
4 10
3 0
10 10
7 0
1 8
4 6
9 8
|
6
3 0
7 0
10 10
4 10
1 8
0 5
|
The example input corresponds to the following figure (with its respective convex hull indicated in blue):
Algorithms and Data Structures (L.EIC011) 2024/2025
DCC/FCUP & DEI/FEUP - University of Porto
 The convex
hull of a set of 2D points is the smallest convex polygon that
encloses all the points. It is a very useful geometric primitive
that can give a rough idea of the shape of the set of points. It
also serves as first preprocessing step to many other geometric
algorithms.
The convex
hull of a set of 2D points is the smallest convex polygon that
encloses all the points. It is a very useful geometric primitive
that can give a rough idea of the shape of the set of points. It
also serves as first preprocessing step to many other geometric
algorithms.