[AED038] Maximum Sum Path

In what concerns the continuous evaluation solving exercises grade during the semester, you should submit until 23:59 of November 30th
(this exercise will still be available for submission after that deadline, but without couting towards your grade)
[to understand the context of this problem, you should read the class #07 exercise sheet]

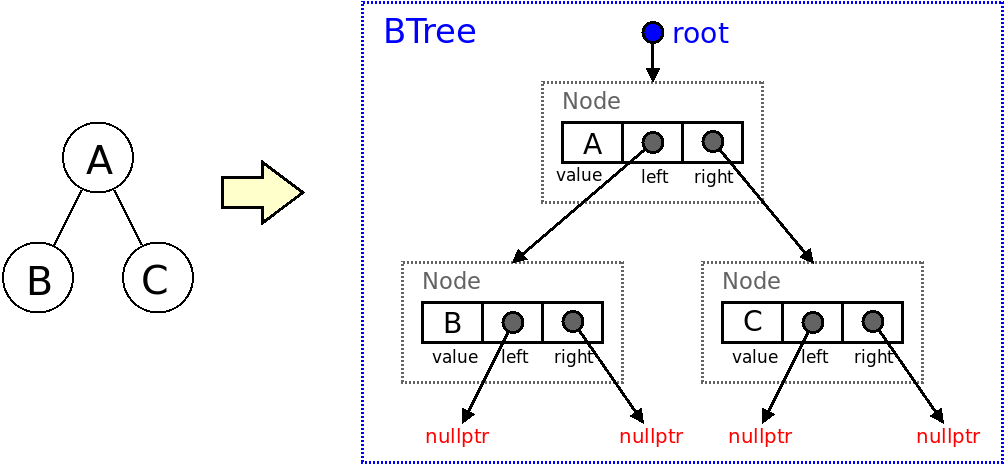
In this problem you should only submit a binaryTree.h file with a self-containing definition of a class BTree<T>

Base Code

Use as a basis the class BTree<T> (see code | download code) which implements a generic binary tree that was explained in classes, with methods to read a tree from standard input, to write several node traversals, to count the number of nodes, to compute the height and to see if it contains a certain value.

The Problem

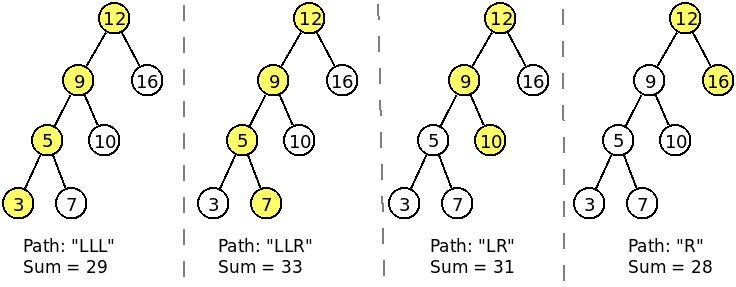
Add a new method std::string maxSum() to the class. The function should return a string containing only the characters 'L' and 'R' indicating the path from a root to a leaf with the largest possible sum of its nodes. 'L' means left and 'R' means right, so for instance "LLR" indicates the path root→left→left→right.

You can assume that the nodes will only contain positive integer values and that always exists a single maximum sum path with at least two nodes for the cases that will be given to your code. The following figure illustrates a binary tree and the 4 possible paths, with the largest sum path being the second one, so the method should return "LLR".

Submission

You should submit the file binaryTree.h with the method maxSum added to binaryTree<T> as requested (and without removing any of the other existing methods). You can however create additional methods, if you need them.

Mooshak will use the following code to link to your class, read the inputs, build the trees and call your method, printing its result.

#include <iostream>
#include <string>
#include <vector>

#include "binaryTree.h"

// Read a tree of ints assuming "N" as the null value
// call t.sumLevels() method and write its output
void read() {
  BTree<int> t;
  t.read("N");
  
  std::cout << "t.maxSum() = \"" << t.maxSum() << "\"" << std::endl;
}

int main() {

  int n;
  std::cin >> n;
  for (int i=0; i<n; i++) read();
  
  return 0;
}

Example Input	Example Output
3 12 9 5 3 N N 7 N N 10 N N 16 N N 6 5 4 3 2 1 N N N N N N N 3 1 N 2 N N 5 N 8 6 N 7 N N 10 N N	t.maxSum() = "LLR" t.maxSum() = "LLLLL" t.maxSum() = "RRLR"